Equation

[yylux]

Bonjour,

Je suis tombé sur cette question:

La somme des carrés de deux nombres impairs consécutifs positifs est 1570. Retrouvez ces nombres.

Je ne sais pas comment ajouter "impair" dans mon équation.



À mon avis j'ai ici la somme (+) des deux carrés (^2) de deux nombres consécutifs (+2)... =1570... mais comment définir l'impair?

Merci d'avance

[WillyCagnes]

bjr
ton equation est bonne pas la peine de te compliquer la vie en posant
(2n+1)²+(2n+3)²=1570

ce que tu as fait c'est bien plus simple
tu poses x=nombre impair (de la forme 2n+1)
et le suivant sera egal à x+2
resoudre x²+(x+2)² =1570 avec x impair de la forme 2n+1

une autre façon de résoudre rapidement, je dis que (x+2)² est voisin de x²
soient 2 x² presque égal à 1570
x= V(1570/2) environ 28
je prends les nombres impairs voisins : 27 et 29
et je vérifie que 27²+29²=1570 ok

[zygomatique]

salut

oui le impair tu peux toujours voir à la fin mais le "impairs consécutifs" conduit à ce +2 dans ce que tu écris ...

quant à la résolution :



et


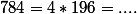
maintenant pour comparer tu peux aussi résoudre l'équation ou (encore mieux) qui se résout très simplement ....