Equation

[R.a.y]

Bonjour,
Pourriez vous me résoudre cette équation pour que je puisse comprendre comment faire.

(2y-3)/8 = (y-4)/6

[Dinozzo13]

Salut !
La politique du forum exige de ne pas faire les devoirs des autres, on peut t'aider à le faire, mais tu ne peux pas ne pas t'investir.

Ton équation est-elle bien : ?
Si oui, alors regroupe et 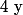d'un côté de l'équation et regroupe les deux fractions de l'autre côté.
Simplifie et tu obtiendras ta solution :zen:

[R.a.y]

Je me douté Mais tant que l'on maide cela me convient :happy2:

Et je vais rectifier l'équation car je l'ai mal écrite

[Dinozzo13]

Ah ok.
Ne t'inquiète pas, on est prêt à t'aider :++:



Effectue le produit en croix :
devient
Développe et regroupe les termes en "" d'un côté et le reste (ne dépendant pas de ) de l'autre côté de l'équation.

[R.a.y]

C'est bon J'ai trouvé :ptdr:
[ du moins il me semble ]

[R.a.y]

Un grand merci a toi [ ou vous ] comme tu prefere

[Dinozzo13]

Ok, si tu as un doute, remplace la valeur de y trouvée et vérifie l'éqgalité dans l'équation initiale.

@+

[R.a.y]

J'ai fait la vérifications et j'ai trouvé -1.25 au deux donc j'en ai déduit que j'avais bon

[Dinozzo13]

:hum: ce n'est pas la bonne solution :

Si alors :

et

donc n'est pas la solution

[R.a.y]

Nan y= -3.5
mais quand l'on fait la vérifications sa nous donne comme résultat ( pour (2y-3)/8 et pour (y-4)/6 ) -1.25

par contre j'aurais un autre problème :

((3y-7)/8)-((5y-1)/16) = ((3-2y)/4)-1
j'avais penser mettre tout au meme dénominateur puis le supprimer se qui donner : 6y-14 = -4-8y

j'aimerais donc savoir si la méthode utilisés et bonne car le résultat trouvé n'est pas le bon quand je vérifie avec le calcul de base

[Dinozzo13]

Moi j'aurai tout réduis sous le dénominateur commun 16.
tu auras donc il faudra donc résoudre

[R.a.y]

Et maintenant me voici bloqué sur celle ci :

[Billball]

bah développe tt ;)

[R.a.y]

Bah se que j'avais fait c'est que j'avais dévelloper et ensuite mis tout au carré pour supprimer les racines mais je bloque sur le résultat

[Dinozzo13]

Salut !

3x²+12x=102 devient 3x²+12x-102=0
En factorisant par 3 : 3(x²+4x-34)=0 d'où x²+4x-34
Or le coefficient des termes en x² et le terme constant -34 étant de signe opposés, il existe à coup sûr deux racines.
Calcule et trouve x' et x''

[R.a.y]

Je suis vraiment bloqué vous pourriez pas me montrez entierement avec un autre calcul comment faire ou essayer de m'aider plus (même si c'est deja bien l'aide que vous m'apportez)

[myself18]

Salut!
Je vais essaiyé de t'aider un peu

Tu es arrivé au résultat: 3x²+12x=102
Cela ne te fais pas pensé a une équation du second degrè?

Donc : 3x²+12x-102=0
Maintenant, tu as du voir en cours comment trouvez les solutions d'une équation de ce type.

Tu dois d'abord calculer le discriminant (le "delta")
puis en fonction, si le discriminant est positif tu as 2 solutions( il y a donc 2 racines simple)
s'il est négatif , il n'y a pas de racines réelles
S'il est nul tu as une seule solution (la racine est dites double)

*J'espere ne pas me tromper dans ce que je raconte*

Le delta se calcul ainsi:
Voici une équation ax²+bx+c=0
Ton discriminant sera: ;)=b²-4ac Si celui si est positif, alors tu as (comme j'ai écrit) deux solutions
x=(-b+(racine;)))/2a

et

x'=(-b-(racine;)))/2a

Voila j'espere que c'est bien ça que tu voulais savoir
Si c'est bien cela il suffit juste que tu appliques a ton equation

ps: désolé pour l'ecriture j'espere que tu comprends quand meme

[R.a.y]

Quand j'ai fait cela j'ai obtenu comme résultat -4.16
et en voulant vérifier sa n'aller pas
alors soit ma méthode de vérifications et mauvaise
soit il y a des erreurs de calculs
soit je me suis tromper en annoncant le résultat trouver et en vériter le résultat est : 3x²+12x-102 = 150
ou autre chose