Equation symétrique du 4émé degré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
dakou
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Oct 2005, 08:58
-
 par dakou » 22 Oct 2005, 09:03
par dakou » 22 Oct 2005, 09:03
Voilà je n'arrive pas à répondre à cette question:
(E) désigne l'équation x^4 -4x^3 +2x² +1 = 0.
1] Démontrez que si x(indice 0) est solution de (E), alors 1/x(indice 0) est solution de (E).
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 22 Oct 2005, 09:14
par becirj » 22 Oct 2005, 09:14
Je crois que dans ton équation il manque un "-4x".
Vérifie ton texte.
-
dakou
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Oct 2005, 08:58
-
 par dakou » 22 Oct 2005, 09:17
par dakou » 22 Oct 2005, 09:17
Lol oui merci, en effet il manque -4x :)
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 22 Oct 2005, 09:53
par cesar » 22 Oct 2005, 09:53
dakou a écrit:Voilà je n'arrive pas à répondre à cette question:
(E) désigne l'équation x^4 -4x^3 +2x²-4x +1 = 0.
1] Démontrez que si x(indice 0) est solution de (E), alors 1/x(indice 0) est solution de (E).
supposes que tu as x1 racine de l'équation, remplace dans l'équation x, par 1/x1 et multiplie le tout par x1^4, que se passe t il ?
-
dakou
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Oct 2005, 08:58
-
 par dakou » 22 Oct 2005, 10:57
par dakou » 22 Oct 2005, 10:57
Désolé mais je ne comprends tjs pas.
Et pourquoi tu changes x0 par x1 ?
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 22 Oct 2005, 12:45
par becirj » 22 Oct 2005, 12:45
Dans l'indication de Cesar, remplace

par

.
Remarque préalable : 0 n'est pas solution de l'équation donc
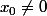
.
Tu peux aussi partir de

solution de l'équation et diviser tous les termes par

et tu obtiendras que

est solution de l'équation.
-
dakou
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Oct 2005, 08:58
-
 par dakou » 22 Oct 2005, 13:13
par dakou » 22 Oct 2005, 13:13
J'y arrive toujours pas.
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 22 Oct 2005, 13:38
par becirj » 22 Oct 2005, 13:38
Je suppose

solution de l'équation :

Je divise par

et je simplifie les quotients

Sachant que
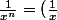^n)
, on trouve que l'équation est vérifiée par

-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 22 Oct 2005, 17:49
par cesar » 22 Oct 2005, 17:49
dakou a écrit:J'y arrive toujours pas.
tu es lourd !!! :marteau: becirj t'a maché tout le travail...
-
dakou
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Oct 2005, 08:58
-
 par dakou » 26 Oct 2005, 07:59
par dakou » 26 Oct 2005, 07:59
En posant X = x + (1/x), comment démontrer que l'équation...
x² -4x + 2 -(4/x) + (1/x²) = 0
...se ramène à une équation du second degré ?
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 26 Oct 2005, 08:13
par becirj » 26 Oct 2005, 08:13
-
dakou
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Oct 2005, 08:58
-
 par dakou » 26 Oct 2005, 08:34
par dakou » 26 Oct 2005, 08:34
Moi je trouve : X²-4X+4
Mais je ne comprend pas pourquoi tu dis que x²+1/x²=(x+1/x)²-2
Pour moi ce n'est pas "moins 2", mais "plus 2".
Merci.
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 26 Oct 2005, 08:43
par becirj » 26 Oct 2005, 08:43
^2=x^2+2\times x\times {1\over x}+({1\over x})^2)
(identité remarquable)
De la on déduit la relation indiquée
-
dakou
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Oct 2005, 08:58
-
 par dakou » 26 Oct 2005, 08:50
par dakou » 26 Oct 2005, 08:50
Mais c'est biensûr ! :id:
Merci. :marteau: :briques: :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
