Bonjour,
j'ai une correction que je n'arrive pas à refaire.
on me dit que:
Gy = (1-W) . Gk + W . Gl
donne
W . (Gl - Gk) = Gy - 1
pour moi ce n'est possible que si on a 1 - (W.Gk) dans la première équation.
merci pour votre aide.
équation simple
11 messages
- Page 1 sur 1
plus précisément c'est Delta y qui vaut Delta x / x
Cela vient de la formule de définition de la dérivée (f(x+h)-f(x))/h qui s'écrit en fait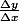 et qui tend vers f'(x) donc pour des intervalles petits on peut dire que
et qui tend vers f'(x) donc pour des intervalles petits on peut dire que
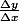 ~ f'(x) et donc que
~ f'(x) et donc que 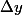 ~f'(x)
~f'(x) 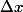
Dans le cas de ta fonction ln x, la dérivée vaut 1/x et donc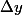 ~
~ 
Cela vient de la formule de définition de la dérivée (f(x+h)-f(x))/h qui s'écrit en fait
Dans le cas de ta fonction ln x, la dérivée vaut 1/x et donc
Aktar a écrit:Plus spécifiquement, peut on dire que log(x)'= x'/x= delta x/x (avec delta qui signifie la variation) ?
Hello,
Je ne vois pas trop quels éléments de réponse tu attends ...
Si x est une fonction, on a bien
Si x est la variable, ton x' n'a pas lieu d'être ...
Peut tu nous dire ce qui t'amène à poser cette question ?
en faite je travaille sur une fonction cobb-douglas, et je raisonne sur des taux de croissance.
et je dois passé d'une relation du type k = K/L à une relation logarithmique pour obtenir le taux de croissance de k
et j'en déduit que log(k)=log (K)-log(L) donne :
(delta k) / k = (delta K) /K - (Delta L) / L
voila c'est juste par convenance, dans un exercice de macroéconomie, que l'auteur utilise c'est expression apparemment. Et moi je cherche une explication assez simple qui puisse justifier ses résultats.
et je dois passé d'une relation du type k = K/L à une relation logarithmique pour obtenir le taux de croissance de k
et j'en déduit que log(k)=log (K)-log(L) donne :
(delta k) / k = (delta K) /K - (Delta L) / L
voila c'est juste par convenance, dans un exercice de macroéconomie, que l'auteur utilise c'est expression apparemment. Et moi je cherche une explication assez simple qui puisse justifier ses résultats.
Il faudrait préciser c'est quoi la variable et par rapport à quoi tu dérives.
Si k, K et L sont des fonctions que tu dérives toutes par rapport à la même variable, alors on a effectivement mais cette écriture est un peu gênante dans le sens ou c'est une variation infinitésimal (le symbole
mais cette écriture est un peu gênante dans le sens ou c'est une variation infinitésimal (le symbole  n'est pas approprié)
n'est pas approprié)
Si k, K et L sont des fonctions que tu dérives toutes par rapport à la même variable, alors on a effectivement
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
