équation du second degré a resoudre ...

[kelly1001]

bonjour,
J'ai une petite équation a résoudre mais j'ai beau la retourner dans tout les sens je vois pas comment faire ... (c'est peut etre tout bête ) mais j'aimerai que quelqu'un m'aide , me guide ..

alors là voilà : 0,3= (10-² +x)² /(10-² -x)(0.1 -x)
trouver x ...

j'ai le résultat du prof mais je tombe jamais dessus ! :mur:
merci d'avance pour votre aide
kelly

[Monsieur23]

0,3= (10-² +x)² /(10-² -x)(0.1 -x)

Donc 0= [(10-² +x)² /(10-² -x)(0.1 -x)] - 0.3

On mets au même dénominateur :


Et une fraction est nulle si et seulement si son numérateur est nul.

[Noemi]

Mettre sous la forme A(x) = 0
Réduire au même dénominateur
Développer le numérateur
Résoudre l'équation du second degré

[kelly1001]

0,3= (10-² +x)² /(10-² -x)(0.1 -x)

Donc 0= [(10-² +x)² /(10-² -x)(0.1 -x)] - 0.3

On mets au même dénominateur :


Et une fraction est nulle si et seulement si son numérateur est nul.

quand je développe le numérateur , je trouve des trucs ... :briques:
je sais que vous m'avez déjà maché le travaille mais si pouviez continuer .. sinon tant pis je me debrouillerai :triste:

[Noemi]

Sauf erreur tu devrais trouver en numérateur : 0,7x^2+0,053x - 0,0002

[axiome]

Une petite correction. Le numérateur doit être nul et le dénominateur, lui, doit être non nul.

[kelly1001]

Sauf erreur tu devrais trouver en numérateur : 0,7x^2+0,053x - 0,0002

ok c ca parce qu'après quand je calcul le discriminant puis la valeur de x on retrouve bien le résultat du prof ...
mais comment vous faites ? parce que moi quand je développe je trouve ²+2.10-²x-0.2999 (je suis chiante ! ) :help:

[Noemi]

je développe le calcul pour le numérateur
10^(-4) +2.10^(-2)x + x^2 - 0,3(10^(-3)-10^(-2)x-10^(-1)x+x^2)
= x^2 -0,3x^2 +2.10^(-2)x + 0,3.10^(-2)x + 0,3.10^(-1)x + 10^(-4) -0,3.10^(-3)
= 0,7x^2 + 0,053 x -0,0002

[Antho07]

Je réécris en latex ce qu'a ecrit Noemie




=

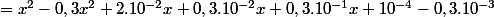
[kelly1001]

je développe le calcul pour le numérateur
10^(-4) +2.10^(-2)x + x^2 - 0,3(10^(-3)-10^(-2)x-10^(-1)x+x^2)
= x^2 -0,3x^2 +2.10^(-2)x + 0,3.10^(-2)x + 0,3.10^(-1)x + 10^(-4) -0,3.10^(-3)
= 0,7x^2 + 0,053 x -0,0002

merci a tous:++:
vraiment ...

[kelly1001]

bon c'est parti je me tape la honte encore une fois, je pensai avoir trouver et quand je refait le calcul bien au propre je me demande que fais t_on du dénominateur???
parce que grâce à vous je trouve 0.7x²+0.053x - 2.10^-4 /(10-² - x)(0.1 -x)

alors oui je développe le dénominateur et après ..

[Noemi]

Inutile de développer le dénominateur.

Une fraction est nulle si son numérateur est égal à 0.