équation second dégré avec puissance en fraction.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 14 Nov 2018, 19:16
par novicemaths » 14 Nov 2018, 19:16
Bonsoir
Est-ce que
^{\frac{1}{4}})
équivaux à
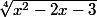
Merci!
A bientôt
-
mathelot
 par mathelot » 14 Nov 2018, 19:26
par mathelot » 14 Nov 2018, 19:26
oui, c'est la même chose, la puissance fractionnaire étant plus facile à manier
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 14 Nov 2018, 19:51
par novicemaths » 14 Nov 2018, 19:51
Je dois étudier le domaine de définition de f.
=(x^2-2x-3)^{\frac{1}[4}})
Il faut que je calcul le discriminant de
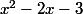
, qui est delta<0.
Donc, Df est R.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 14 Nov 2018, 20:05
par pascal16 » 14 Nov 2018, 20:05
delta < 0, vraiment ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 14 Nov 2018, 20:14
par novicemaths » 14 Nov 2018, 20:14
Merci, vous m'avez aider à trouver une erreur d'inattention dans mon calcul!
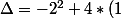*(-3)=4+12=16)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités