Equation produit nul
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 16:35
par princessedeval » 24 Nov 2013, 16:35
Bonjour,
Pour le Jeudi 28 novembre, j'ai un DM de maths sur les produits nul et j'ai un petit doute sur les équations produit.
Voici un de mes exercices :
100x²-36=0
J'ai donc fait la démarche suivante :
(10x)²-6²=0
(10x-6)(10x+6)=0 (j'ai utilisé les identités remarquable)
ensuite je fait : 2 équations -> (10x-6) = 0 puis une autre (10x+6) = 0
J'ai donc trouvé 2 solutions.
Mais à une autre questions, c'est là que je bloque voici l'énoncé :
16x²-48x+36 = 0
Je me suis dit que 16x² = (4x)² et que 36 = 6² mais 48x ? Comment faire ? Est-il possible de résoudre une équation produit comme ceci : x(16x-48) + 36 = 0?
Merci de bien vouloir m'aider
Princessedeval
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 16:38
par mcar0nd » 24 Nov 2013, 16:38
princessedeval a écrit:Bonjour,
Pour le Jeudi 28 novembre, j'ai un DM de maths sur les produits nul et j'ai un petit doute sur les équations produit.
Voici un de mes exercices :
100x²-36=0
J'ai donc fait la démarche suivante :
(10x)²-6²=0
(10x-6)(10x+6)=0 (j'ai utilisé les identités remarquable)
ensuite je fait : 2 équations -> (10x-6) = 0 puis une autre (10x+6) = 0
J'ai donc trouvé 2 solutions.
Mais à une autre questions, c'est là que je bloque voici l'énoncé :
16x²-48x+36 = 0
Je me suis dit que 16x² = (4x)² et que 36 = 6² mais 48x ? Comment faire ? Est-il possible de résoudre une équation produit comme ceci : x(16x-48) + 36 = 0?
Merci de bien vouloir m'aider
Princessedeval
Salut, pour la deuxième équation, quel est le diviseur commun de 16 ; -48 et 36?
-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 16:40
par princessedeval » 24 Nov 2013, 16:40
mcar0nd a écrit:Salut, pour la deuxième équation, quel est le diviseur commun de 16 ; -48 et 36?
Je pense que le diviseur commun de 16, -48 et 36 est 4 ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 16:41
par mcar0nd » 24 Nov 2013, 16:41
princessedeval a écrit:Je pense que le diviseur commun de 16, -48 et 36 est 4 ?
Exactement, donc en mettant 4 en facteur, tu trouves quoi?

-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 16:43
par princessedeval » 24 Nov 2013, 16:43
mcar0nd a écrit:Exactement, donc en mettant 4 en facteur, tu trouves quoi?

Je trouve : 4x(4x-12) +36 = 0 ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 16:44
par mcar0nd » 24 Nov 2013, 16:44
princessedeval a écrit:Je trouve : 4x(4x-12) +36 = 0 ?
Oui, mais ce n'est pas vraiment ce que j'attendais en fait.
Mets juste 4 en facteur, tu vas trouvé quelque chose comme
=0)
.

-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 16:47
par princessedeval » 24 Nov 2013, 16:47
mcar0nd a écrit:Oui, mais ce n'est pas vraiment ce que j'attendais en fait.
Mets juste 4 en facteur, tu vas trouvé quelque chose comme
=0)
.

AHHHH !!! Donc 4(4x²-12+9) = 0 ? Si oui, comment après on peux résoudre l'équation produit ?? Vue qu'il y a 4x² ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 16:50
par mcar0nd » 24 Nov 2013, 16:50
princessedeval a écrit:AHHHH !!! Donc 4(4x²-12+9) = 0 ? Si oui, comment après on peux résoudre l'équation produit ?? Vue qu'il y a 4x² ?
Attention, c'est
=0)
, sûrement une faute de frappe.

Maintenant, tu devrais reconnaitre une identité remarquable dans

.

-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 16:56
par princessedeval » 24 Nov 2013, 16:56
mcar0nd a écrit:Attention, c'est
=0)
, sûrement une faute de frappe.

Maintenant, tu devrais reconnaitre une identité remarquable dans

.

Je pense soit (a+b)² soit (a-b)² mais ça ne peux pas marquer dans les deux cas car +48x serait 48x dans les deux cas... :-/
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 16:59
par mcar0nd » 24 Nov 2013, 16:59
princessedeval a écrit:Je pense soit (a+b)² soit (a-b)² mais ça ne peux pas marquer dans les deux cas car +48x serait 48x dans les deux cas... :-/
N'oublie pas que ton équation initiale est
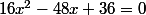
, et tu as montre qu'elle est équivalente à
=0)
.
Il faut maintenant que tu factorise

, en reconnaissant une identité remarquable; ici tu remarque que tu as quelque chose de la forme
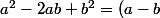^2)
, il te reste à trouver a et b.

-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 17:08
par princessedeval » 24 Nov 2013, 17:08
mcar0nd a écrit:N'oublie pas que ton équation initiale est
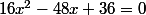
, et tu as montre qu'elle est équivalente à
=0)
.
Il faut maintenant que tu factorise

, en reconnaissant une identité remarquable; ici tu remarque que tu as quelque chose de la forme
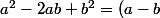^2)
, il te reste à trouver a et b.

C'est (2x-3)² ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 17:08
par mcar0nd » 24 Nov 2013, 17:08
princessedeval a écrit:C'est (2x-3)² ?
Exactement, donc ton équation devient quoi au final?

-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 17:11
par princessedeval » 24 Nov 2013, 17:11
mcar0nd a écrit:Exactement, donc ton équation devient quoi au final?

Donc (2x-3)² = 0
Donc (2x-3)(2x-3) = 0
Donc (2x-3) = 0
2x = 3
x = 1.5
Il y a qu'une seule solution ? 1,5 ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 17:12
par mcar0nd » 24 Nov 2013, 17:12
princessedeval a écrit:Donc (2x-3)² = 0
Donc (2x-3)(2x-3) = 0
Donc (2x-3) = 0
2x = 3
x = 1.5
Il y a qu'une seule solution ? 1,5 ?
Attention, ton équation s'écrit
^2=0)
, et oui, il n'y a qu'une seule solution qui est bien celle que tu as donnée.

-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 17:16
par princessedeval » 24 Nov 2013, 17:16
mcar0nd a écrit:Attention, ton équation s'écrit
^2=0)
, et oui, il n'y a qu'une seule solution qui est bien celle que tu as donnée.

Je comprend pas pourquoi vous avez mis 4 devant (2x-3)² ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 24 Nov 2013, 17:20
par mcar0nd » 24 Nov 2013, 17:20
princessedeval a écrit:Je comprend pas pourquoi vous avez mis 4 devant (2x-3)² ?
On a dit que ton équation
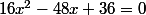
pouvait s'écrire
=0)
et que
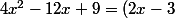^2)
; donc en injectant ça dans la deuxième écriture de l'équation initiale, on trouve
^2=0)
.

-
princessedeval
- Membre Naturel
- Messages: 51
- Enregistré le: 23 Oct 2013, 14:10
-
 par princessedeval » 24 Nov 2013, 17:21
par princessedeval » 24 Nov 2013, 17:21
mcar0nd a écrit:On a dit que ton équation
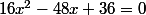
pouvait s'écrire
=0)
et que
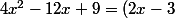^2)
; donc en injectant ça dans la deuxième écriture de l'équation initiale, on trouve
^2=0)
.

D'accord

Merci beaucoup de votre aide

J'ai maintenant compris comment résoudre ce genre d'équation produit

Encore merci !!




Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
