Equation pour trouver point d'intersection

[gorillette]

Bonsoir,

On considère la droite Dn dont y=-2x+n pour tout réel n.
Et la courbe P dont y=x²-4x+1

a. tracer deux droites D0 et D8 dont n=0 et n=8 et la courbe P
b. determiner par des calculs le nombre de points d'intersection de Dn et de P suivant les valeurs de n.

Donc le a. j'ai réussi mais le b. je n'ai pas compris, est ce qu'il faut faire une equation -2x+n = x²-4x+1 ?
ou faire des equations a deux inconnues en utilisant D0 et D8 ?

C'est pour demain. ^^

Merci

[chan79]

Bonsoir,



-2x+n = x²-4x+1 ?



Merci

Bonsoir
oui, résouds cette équation du second degré

[gorillette]

Donc ca fait; -x²+2x-1= -n ou -x²+2x-1+n=0 ?
Des deux facons je n'arrive pas a avancer a cause du n. :/


edit: je devrais calculer delta= b²-4ac donc 4-4*-1*-1= 0 ;) qu'une solution; x0 = -b/2a = -2/-2=1

alors -1²+2*1-1 = -n
1+2-1 + n = 0
2+n = 0
n = -2 ??

[Kikoo <3 Bieber]

Donc ca fait; -x²+2x-1= -n ou -x²+2x-1+n=0 ?
Des deux facons je n'arrive pas a avancer a cause du n. :/

Ben n c'est un nombre, un paramètre.
Tu résous normalement sans tenir compte du n : écris-le et laisse-le tranquille.

[Dlzlogic]

On vous demande le nombre de points d'intersection.
La résolution de l'équation est le moyen d'y arriver.
Combien y a-t-il de solutions à une équation du second degré ?

[gorillette]

Bonsoir,
j'étais en train d'éditer mon post ... c'est ça ?

[Kikoo <3 Bieber]

Donc ca fait; -x²+2x-1= -n ou -x²+2x-1+n=0 ?
Des deux facons je n'arrive pas a avancer a cause du n. :/


edit: je devrais calculer delta= b²-4ac donc 4-4*-1*-1= 0 qu'une solution; x0 = -b/2a = -2/-2=1

alors -1²+2*1-1 = -n
1+2-1 + n = 0
2+n = 0
n = -2 ??

C'est pas bon pour le Delta. Que vaut c dans ton exo ?

[gorillette]

euh c= -1 ou j'ai mal calculer donc ca ferait; x²-2x+1-n = 0 donc c= 1 ?

[Kikoo <3 Bieber]

euh c= -1 mais si c'est juste la fonction de P alors c=1

Non et non.

c vaut ici n-1 !

[chan79]

euh c= -1 mais si c'est juste la fonction de P alors c=1

il faut que tu déterminer le nombre de solution de
x²-2x+1=n
soit
(x-1)²=n
que peut-tu dire si n0 ?

[gorillette]

Ah donc comment je calcule delta si c= n-1 ?

[chan79]

Ah donc comment je calcule delta si c= n-1 ?

pas besoin de delta dans ce cas, même si on peut faire avec

[gorillette]

Chan79 je n'ai pas compris pourquoi tu écris la forme factorisée.
euh si n<0 alors pas de solution, si n>0 alors deux solutions et si n=0 1 solution ?

[chan79]

Chan79 je n'ai pas compris pourquoi tu écris la forme factorisée.
euh si n0 alors deux solutions et si n=0 1 solution ?

voilà, tu as bien répondu; pas besoin de delta si on ne te demande que le nombre de solutions suivant les valeurs de n

[Kikoo <3 Bieber]

Ah donc comment je calcule delta si c= n-1 ?

Ben je vois pas le problème, tu appliques
Réfléchis à cette méthode (académique : celle qu'attend sans doute ton/ta prof) et à celle de Chan.

[gorillette]

Chan79 aah si simple que ca je m'embarquais pour determiner les points d'intersection.
Kikoo <3 bieber merci comme ca je saurais !

et chan79, si tu as mis la forme factorisée c'était pour me faire comprendre le nombre de solution ?
Parce que dans ma copie c'est écrit "justifier", je me dis que c'est peut etre ça la justification !

[Kikoo <3 Bieber]

[quote="gorillette"]Chan79 aah si simple que ca je m'embarquais pour determiner les points d'intersection.
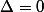
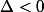
Kikoo 0[/TEX], et , et on a la satisfaction de voir que l'explication est la même !
Mais la méthode Chan est plus immédiate

[Kikoo <3 Bieber]

et chan79, si tu as mis la forme factorisée c'était pour me faire comprendre le nombre de solution ?
Parce que dans ma copie c'est écrit "justifier", je me dis que c'est peut etre ça la justification !

L'explication c'est :

(ax+b)²=cte
Si cte=0 alors on a (ax+b)=cte ou (ax+b)=cte
C'est redondant. Donc un point unique d'intersection avec l'axe des abscisses dont l'abscisse vaut x=-b/a

Si cte>0, alors on a (ax+b)²-cte=0 avec cte=(\sqrt{cte})²
en factorisant : (ax+b-\sqrt{cte})(ax+b+\sqrt{cte})=0
d'où deux solutions.

Si cte<0, alors on a (ax+b)²<0 ce qui est impossible...

[gorillette]

euh ca veut dire quoi cte ? ^^

[Kikoo <3 Bieber]

euh ca veut dire quoi cte ? ^^

Constante.

Pour ce que tu as écrit avant de modifier, j'ai apporté la justification. Il suffit de lire.