Equation de plan

[Rubynette28]

Bonjour, je bloque sur une question et j'aurais voulu savoir si quelqu'un pouvait me donner un coup de pouce pour la résoudre.
Si a,b,c≠0, quelle est l'équation du plan passant par les points A(a,0,0) B(0,b,0) et C(0,0,c) ?

Merci d'avance.

[Yezu]

Salut,

Je ne sais pas si le produit vectoriel est de niveau Lycée dans le système français; si oui c'est évident. Il suffit de faire le produit vectoriel entre 2 vecteurs quelconques AB, BC ou AC) pour en déduire un vecteur normal au plan. L'équation s'en suit.

Si ça ne l'est pas : on pose
vecteur normal au plan avec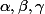 réels non-simultanément nuls.

Comme le vecteur est normal au plan, il est orthogonal à tout vecteur appartenant au plan. Que peux-tu en déduire sur les produits scalaires entre ce vecteur normal et un vecteur quelconque appartenant au plan ?
Calcule ensuite le produit scalaire entre ce vecteur normal et des vecteurs quelconques formés à partir des points A, B et C. Tu pourras en déduire un système d'équations qui te permettra de trouver les coordonnées du vecteur normal n et d'en déduire l'équation du plan.

[mathelot]

une équation du plan (ABC) est

[Rubynette28]

Ok merci bcp à vous deux.

Non je n'ai pas vu le produit vectoriel.

Si je pose le vecteur normal, on a donc un produit scalaire égal à 0, en résolvant le système je trouve .
J'ai donc une équation x+y+z+d=0 avec dR
Sachant que A appartient au plan j'ai donc a=-d
de meme pour B : b=-d
et pour C : c=-d
Et je ne vois pas comment parvenir au résultat..
Je suis désolée je crois que je bloque sur un truc tout bête

[Yezu]

Salut,

On a :


En faisant les produits scalaires et ; on obtient :

Si on considere comme parametre, alors :

Les coordonnes du vecteur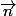 sont ainsi de la forme :

avec .

Pour , on retrouve l'equation de mathelot.

Edit : dans le premier systeme, il y a un devant le et dans le second, le premier membre de l'egalite est

[Pseuda]

Bonjour,

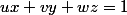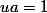Ou bien, la méthode immédiate : on pose , l'équation du plan (de terme constant égal à 1), et on dit que A, B et C au plan. On a donc , soit , etc...

Petite précaution : on a le droit de poser cette équation car on peut diviser tous les coefficients du plan par son terme constant pour obtenir une équation de terme constant égal à 1 ; et ce terme constant est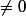 car O n'appartient pas au plan (pourquoi ?).

Mais la méthode de Yezu est préférable, justement pour ne pas avoir à montrer que O n'appartient pas au plan.