Equation irrationnelle

[koddo]

resoudre x-a = racine carrée de 8-x (a appartenant à R )

[chan79]

resoudre x-a = racine carrée de 8-x (a appartenant à R )

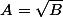
Utilise équivaut à

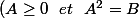[WillyCagnes]

bonsoir,
avec
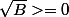
équivaut à x<=8

[koddo]

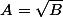
Utilise équivaut à

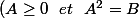on a donc x;)a et (x-a);)^2= x-8

[chan79]

on a donc x;)a et (x-a);)^2= x-8

Commence par résoudre (x-a)²=8-x

[koddo]

Commence par résoudre (x-a)²=8-x

On obtient x^2-(2a-1)x +a^2-8=0

=;)(2a-1);)^2-4(a^2-8)=-4a+33
>0;)a<33/4
Pour a<33/4 on x=(2a-1-;)(-4a+33))/2 et x^'=(2a-1+;)(-4a+33))/2
La seule solution qui remplit la condition x;)a est x'
sauf erreur

[chan79]

On obtient x^2-(2a-1)x +a^2-8=0

=;)(2a-1);)^2-4(a^2-8)=-4a+33
>0;)a<33/4
Pour a<33/4 on x=(2a-1-;)(-4a+33))/2 et x^'=(2a-1+;)(-4a+33))/2
La seule solution qui remplit la condition x;)a est x'
sauf erreur

salut
c'est presque ça
pour a=8.2 par exemple (qui est inférieur à 33/4), il n'y a pas de solution

[koddo]

[quote="chan79"]salut
c'est presque ça
pour a=8.2 par exemple (qui est inférieur à 33/4), il n'y a pas de solution[/QUOT
Donc a doit etre inférieur à 8
Donc à chaque fois c'est la meme démarche

[chan79]

salut
c'est presque ça
pour a=8.2 par exemple (qui est inférieur à 33/4), il n'y a pas de solution[/QUOT
Donc a doit etre inférieur à 8
Donc à chaque fois c'est la meme démarche

c'est ça. Si a8 pas de solution

Cas particulier: si a=8 alors x=8

[koddo]

c'est ça. Si a<=8, il y a une unique solution, celle que as indiquée.

Merci par curiosité j'ai essayé cette équation et voila ce que j'obtiens:
(8-x^2 )=x-a donc les conditions x;)[-2;)2;2;)2]et x;)a
Ensuite 8-x^2=(x-a)^2 ce qui donne 2x^2-2ax+a^2-8=0
^'=16-a^2 0 dans l’intervalle [-4 ;4]
x=(a-;)(16-a^2 ))/2 et x'=(a+;)(16-a^2 ))/2
x';)a si a;)]-;);-2;)2];)]2;)2;+;)[ or a;)[-4;4]
Donc x’;)a si a;)[-4;-2;)2];)[2;)2;4]
Je crois il reste à vérifier si x’ [-2;)2;2;)2]