Equation à 3 inconnues à résoudre dans Z

par **guigui51250** » 28 Nov 2008, 20:16

Bonjour tout le monde,

Voici mon exercice :

Existe-t-il des entiers relatifs x, y, z tels que x²-3y²-4z²=3

Ce n'est pas un exo que j'ai à faire, c'est un exo qu'il y a dans mon livre de spé dans la partie "prendre toutes les initiatives" et j'aimerais savoir si beaucoup de lycéens arrivent à aborder ce genre d'exo

Bonne soirée

par **lapras** » 28 Nov 2008, 20:22

Salut,
x² = 3(y²+1) mod 4
Sachant qu'un carré est congru a 0 ou 1 mod 4, conclue.

par **guigui51250** » 28 Nov 2008, 20:33

euh j'en conclue qu'il n'y a pas de solution dans Z... c'est ça?

par **Zweig** » 28 Nov 2008, 20:42

Salut,

Oui, car

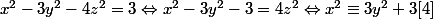
Or un carré est congru à 0 ou 1 mod 4, donc

, impossible.

par **guigui51250** » 28 Nov 2008, 20:52

Ok merci et euh pour ma question principale : a votre avis est-ce facile à aborder pour un élève de terminale? (qui n'est pas "fana" des maths, genre qui n'est pas sur un forum de maths par exemple lol)

par **Zweig** » 28 Nov 2008, 20:55

Bah écoute, c'est relatif ! Si déjà il n'a pas en tête cette propriété des carrés (qui nous pousse à raisonner mod 4), à moins qu'il ne la trouve en tâtonnant, ça peut être dur en effet ...

par **lapras** » 29 Nov 2008, 07:03

Ca dépend du prof...
S le prof lui a fait faire quelques équa diophantiennes, l'élève aura peut etre l'idée de raisonner modulo quelquchose. Le modulo 4 n'est pas caché avec le coefficient devant le z.

par **guigui51250** » 29 Nov 2008, 08:28

Les équations diophantiennes on n'en a pas encore fait, ça viendra peut-être... en tout cas je ne connaissais pas cette methode du modulo 4 qui est assez interessante

Equation à 3 inconnues à résoudre dans Z

Equation à 3 inconnues à résoudre dans Z

Qui est en ligne