Bonjour,
Voici le calcul en question :
4^x - 3^[x+1/2] = 3^[x-1/2] - 2^2x
J'ai simplifié de cette manière :
4^x + 2^2x =3^[x-1/2] + 3^[x+1/2]
4^x + 2^2x =(1 + 1/3). 3^[x+1/2]
2.(4^x) = 4/3.(3^x+1/2)
3(4^x) = 2(3^x+1/2)
log(3) + x.log(4) = log(2) + (x+1/2).log(3)
log(3) + x.log(4) = log2 + x.log(3) + 1/2log(3)
x.log(4) – x.log(3) = log(2) + 1/2log(3) – log(3)
x.log(4/3) = log(2/3) + 1/2log(3)
Cependant, une fois arrivé à la dernière ligne, je me retrouve un peu bloqué. J'ai sans doute dû louper quelque chose de simple ou m'être compliqué la vie pour rien. Il n'empêche que je ne sais pas comment poursuivre le calcul.
Je demande donc votre aide bienveillante !
équation exponentielle à plusieurs degrés différents
3 messages
- Page 1 sur 1
Re: équation exponentielle à plusieurs degrés différents
Tu as fait toutes les étapes compliquées, à priori sans erreur ; tu arrives à une équation de la forme ax=b, et tu dis que tu n'arrives pas à isoler x ?
Re: équation exponentielle à plusieurs degrés différents
Bonjour ;
Tu as trouvé :=ln(\dfrac{2}{3}) + \dfrac{1}{2}ln(3)) , ce qui est juste .
, ce qui est juste .
Maintenant tu peux remarque que :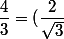^2) et
et  = ln(\sqrt 3})) ;
;
ce qui simplifiera grandement ton expression .
Tu as trouvé :
Maintenant tu peux remarque que :
ce qui simplifiera grandement ton expression .
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
