Equation et étude de fonction

[rmax505]

Bonjour voila un exercice où je n'arrive à rien faire est ce que quelq'un peut m'aider ? SVP
On condière la fonction f définie sur R par :
f(x)=(x+2/3)e^(-3x) + x - 2/3

Déterminer les limites de f en +infini et -infini

Calculer f'(x) et f''(x)
En déuire de variation de f'
Montrer que f'(x) garde un sine constant
Dresser le tableau de variation de la fonction f

Démontrer que la droite d d'équation y=x - (2/3) est asymptote à la courbe C
Préciser la postion de C par rapport à d

Je prends toutes les aides possibles, svp

[Nightmare]

Bonjour

Qu'est-ce que tu n'arrives pas à faire? Cet exercice est très théorique et certaines réponses sont directes si tu as appris ton cours :lol3:

[Elsa_toup]

Bonjour,

1). exp l'emporte sur x.
Donc en , exp(-3x) -> 0 et x-> +, donc f(x) -> 0.
En -, (x+2/3) -> -, exp(-3x) -> , donc leur produit -> -.
On additionne alors x-2/3 qui tend vers -.
Donc en -, f(x) -> -.

2). f '(x) = .
f' '(x) = .

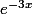3). > 0.
Donc f ''(x) > 0 pour x > 0 et f ''(x) 0 et décroissante pour x = 0 pour tout x.
Donc f croissante pour tout x.
(ce qui est confirmé par ce qu'on atrouvé pour les limites au début).

4). Regarde la limite de f(x) - [x-(2/3)] en + et - .
Puis étudie le signe de cette expression.

Bon courage !

[Nightmare]

1). exp l'emporte sur x.

La justification est maigre ...

[Elsa_toup]

Oui je sais (elle en a de la chance cette justification :ptdr: ).
C'était pour donner une piste, et une idée du résultat.
Mais j'aurais du préciser que mes réponses ne suffisent pas.
Il faut les argumenter.