l'algorithme de la division euclidienne n'est qu'un algorithme de la division
parmi toutes les divisions il n'y en a qu'une seule qui soit euclidienne et sa caractérisation est que le reste est inférieur au diviseur
j'aurais très bien pu commencer comme ben314 dans son premier post :
au lieu de partir de la division euclidienne 666 = 245 * 2 + 176 j'aurais pu faire 666 = 245 * 3 - 69 (qui est une division)
j'aurais alors trouvé une autre solution particulière ....
une équation diophantienne admet une infinité de solutions ... et tout le problème est d'en trouver une ... (et il n'y en a pas de "minimale")
comme je l'ai dit j'utilise aussi l'algorithme de la division !!!! et je sais ne pas me limiter à la division euclidienne même si c'est ce que j'ai fait dans mes exemples .... c'est à dire utiliser l'algorithme d'Euclide étendu comme l'appelle ben314
soit la relation 666x + 245y = 2
et considérons dans
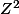
le vecteur
 \ et \ v_1 = (x, y))
on veut que le produit scalaire

REM :: u_1 est en ligne et v_1 est en colonne
on considère alors la matrice

cette matrice est inversible dans
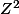
puisque son déterminant 1 l'est et son inverse est la matrice

alors trivialement
\cdot \begin{pmatrix}x \\ y \end{pmatrix} = 2 \( (666,245)M \) \cdot \( M^{-1} \begin{pmatrix} x \\ y \end{pmatrix}\) = 2)
voila où est la magie .... simplement être initié comme dirait l'autre .... non simplement le savoir ...
et la matrice M est une division (ici la division euclidienne) appliquée au couple (666, 245)
et ça se programme très simplement puisque ::
-2 = - E(666/245) et 176 = 666 - 2*245 ou encore pour généraliser 666 = 245q + r
on remarquera que l'inverse de la matrice M = (1 0 \\ -q 1) est (1 0 \\ q 1)
quand on divise la première coordonnée par la deuxième
si on divise la deuxième par la première alors la matrice M est (1 -q \\ 0 1) et son inverse est (1 q \\
0 1)
donc il est aisé de créer un algorithme (en divisant toujours la plus grande coordonnée par la plus petite) qui s'arrête lorsque le reste est nul .... (tout comme pour la division euclidienne)
tout la difficulté est de voir et comprendre que je ne fais que la même chose que ben314 ....
et je rappelle qu'en math spé on voit les matrices qui sont au programme ....
...
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
