[hors programme] équation diophantienne ?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lol37
- Membre Relatif
- Messages: 139
- Enregistré le: 17 Avr 2010, 13:39
-
 par lol37 » 17 Avr 2010, 21:14
par lol37 » 17 Avr 2010, 21:14
Salut à tous

Quelqu'un a la méthode pour résoudre une équation diophantienne avec des fractions ?

 \in \mathbb{Z^2})
Merci de votre aide

lol37.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 17 Avr 2010, 21:58
par Zweig » 17 Avr 2010, 21:58
En dégageant la fraction, on se ramène à une équation du second degré d'inconnue

et de paramètre

:
y - 2x-2 = 0)
Son discriminant vaut
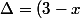^2 + 8x + 8 = (x+1)^2 + 16)
Un condition nécessaire (mais non suffisante !) pour que

est que

. On est donc ramené à déterminer tous les couples
\in\mathbb{Z}\times\mathbb{N})
vérifiant :
^2 + 16 = a^2)
Sauf que, as-tu vu toute la théorie autour des équations du type

?
Un autre méthode consiste à réécrire l'équation sous la forme
(cy+d)=e)
, où les constantes sont à déterminer par identification (si elles existent !).
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 18 Avr 2010, 08:59
par benekire2 » 18 Avr 2010, 08:59
maintenant il faut finir avec les triplets pythagoriciens ! [Zweig t'as beaucoup avancé :zen: ]

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 18 Avr 2010, 14:07
par Olympus » 18 Avr 2010, 14:07
Zweig a écrit:Un condition nécessaire (mais non suffisante !) pour que

est que

.
Euh je ne me connais pas beaucoup en arithmétique dans Z, mais t'es sûr que ce n'est pas plutôt

et que

doit donc être un carré parfait ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 18 Avr 2010, 14:15
par Zweig » 18 Avr 2010, 14:15
Oui pardon, c'est bien sûr la racine du discriminant qui doit être un nombre entier, mea culpa !
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 19 Avr 2010, 17:59
par lapras » 19 Avr 2010, 17:59
Benekire : surtout pas,
si tu as x²+16=y², tu as (x-y)(x+y)=2^3 puis tu regardes les diviseurs de 2^3 ca va tres vite.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 19 Avr 2010, 18:05
par benekire2 » 19 Avr 2010, 18:05
c'est plutôt (y-x)(x+y)=16
mais oui effectivement, c'est beuacoup mieux :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités