Bonjour,
J'ai résolu l'équation differentielle 4y''+9y=0
Solution
E(x)=Omega*A*cos(omega*x)+Omega*b*sin(omega*x)
E'(x)=-AOmega*sin(omega*x)+BOmega*cos(omega*x)
J'ai "déterminer la solution particulière f de l'equation differentielle (E) vérifiant les conditions:
f(0)=1 et f'(2*pi)=3/2
J'avais essayé de résoudre A et B mais je m'emmêle a chaque fois que j'essaye y'aurait t'il une âme charitable pour m'expliquer pas à pas?
Equation Differentielle second ordre
12 messages
- Page 1 sur 1
Re: Equation Differentielle second ordre
Bonjour,
- Que signifient tes "Omega" et "omega" ?
et
sont tes conditions initiales ?
Re: Equation Differentielle second ordre
samoufar a écrit:Bonjour,
- Que signifient tes "Omega" et "omega" ?
et
sont tes conditions initiales ?
C'est le signe
Elles sont données au point 2 de l'exercice avant résoudre l'équation differentielle en 1.
y est une fonction numérique de la variable réelle t définie et deux fois dérivable sur l'ensemble R des nombres réels. Sachant que j'ai pour réponse
f(t)=k(1)*cos(3/2t)+k(2)*sin (3/2t) pour la 1
f(t)=cos (3/2t)-sin(3/2t) pour la 2
J'aimerai savoir comment ils sont arrives là?
Re: Equation Differentielle second ordre
salut
un w comme dans wagon ne suffit-il pas ?
et rend lisible et propre un truc dégueulasse ....

un w comme dans wagon ne suffit-il pas ?
et rend lisible et propre un truc dégueulasse ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Equation Differentielle second ordre
Je sais bien ce que signifie omega, ce que je voulais savoir, c'est
 (dans tous les cas il y avait une erreur dans ta dérivée du premier message
(dans tous les cas il y avait une erreur dans ta dérivée du premier message  , il manque des omega avec minuscule ).
, il manque des omega avec minuscule ).
Bref, sinon, résumons.
Tu as l'équation différentielle : 4y''+9y=0) qui peut se réécrire sous la forme
qui peut se réécrire sous la forme  : y''+\left(\frac{3}{2}\right) ^2 y=0) (si tu as fait un peu de physique alors tu devrais reconnaitre l'équation d'un oscillateur harmonique
(si tu as fait un peu de physique alors tu devrais reconnaitre l'équation d'un oscillateur harmonique  , sinon... équation caractéristique et tout ce qui suit
, sinon... équation caractéristique et tout ce qui suit  ) et tu trouves des solutions de la forme
) et tu trouves des solutions de la forme
+B\sin (\omega t)) avec
avec 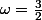 .
.
Tu cherches alors la fonction qui satisfait les conditions initiales=1) et
et =\frac{3}{2}) , c'est ça ?
, c'est ça ?
Si oui, alors il suffit de dériver et à l'aide de tes conditions initiales tu obtiens un système à deux inconnues
et à l'aide de tes conditions initiales tu obtiens un système à deux inconnues  et
et  qu'il suffit de résoudre
qu'il suffit de résoudre 
- Si Omega (avec majuscule) est la même chose que omega (avec minuscule) ;
- Que signifient ces paramètres qui ne sont visiblement pas introduits par l'exercice (du moins si Omega
omega) ?
Bref, sinon, résumons.
Tu as l'équation différentielle
Tu cherches alors la fonction qui satisfait les conditions initiales
Si oui, alors il suffit de dériver
Re: Equation Differentielle second ordre
oui Les 2 Oméga sont les mêmes j'ai la fonction dérive qui est -Aomega*sin(omega x)+Bomega*cos(omega x) le problème c que le calcul me pose problème je n'arrive pas à trouver un A et B cohérents qui me permettront d'affirmer que f(0)=1 et f'(2pi)=3/2 en bref c les systèmes qui me osent problème alors que j'ai pas ce problème pour résoudre k dans ke^-at pour les équations du premier ordre.
Re: Equation Differentielle second ordre
Tes fonctions sont correctes.
Evalues en
en  et
et  en
en 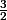 à l'aide des expressions et des valeurs que tu as. Tu obtiens alors un système à deux équations et deux inconnues
à l'aide des expressions et des valeurs que tu as. Tu obtiens alors un système à deux équations et deux inconnues  et
et  qui est alors simple à résoudre.
qui est alors simple à résoudre.
Evalues
Re: Equation Differentielle second ordre
zygomatique a écrit:salut
un w comme dans wagon ne suffit-il pas ?
et rend lisible et propre un truc dégueulasse ....
visiblement certains ne comprennent pas que je m'adresse à eux ...
et d'autres ne comprennent pas que je ne m'adresse pas à eux ....

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Equation Differentielle second ordre
Et certains ne se donnent même pas la peine de faire un effort pour écrire leurs questions correctement en lisant le guide: guide-utilisation-f41/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html
Et certains (mêmes) ne se soucient pas si c'est dans la bonne section ou pas.
Et certains (mêmes) ne se soucient pas si c'est dans la bonne section ou pas.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Equation Differentielle second ordre
@zygomatique : Je sais bien à qui tu t'adresses ne t'en fais pas  . Je disais juste à @PTuner que ce n'est pas la signification de "omega" que je cherchais à connaitre mais plutôt la différence entre "Omega" et "omega" (je suis sensible à la casse, moi
. Je disais juste à @PTuner que ce n'est pas la signification de "omega" que je cherchais à connaitre mais plutôt la différence entre "Omega" et "omega" (je suis sensible à la casse, moi  ).
).
@Lostounet : C'est vrai que c'est plus beau (et surtout plus lisible et plus compréhensible) quand c'est bien écrit (vive LaTeX au passage ). Et oui j'ai vu pas mal de (hors) sujets qui trainaient dans la section Présentation
). Et oui j'ai vu pas mal de (hors) sujets qui trainaient dans la section Présentation 
@Lostounet : C'est vrai que c'est plus beau (et surtout plus lisible et plus compréhensible) quand c'est bien écrit (vive LaTeX au passage

Re: Equation Differentielle second ordre
Je suis de mauvaise humeur today aussi xD
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Equation Differentielle second ordre
Lostounet a écrit:Je suis de mauvaise humeur today aussi xD
ça va mieux ?
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
