[Term S] équation différentielle (Euler...)
34 messages
- Page 1 sur 2 - 1, 2
[Term S] équation différentielle (Euler...)
Coucou tout le monde, voila j'ai un exercice sur la méthode d'Euler, mais je n'ai pas trés bien saisie la méthode... Donc je n'arrive pas l'exo qui suit, mais néanmoins en cours on a fait un TD sur la méthode et l'on devait calculer les tangente por la solution approchée mais la je ne sais pas si c'est bon...
:hein:
Exercice :
On considere l'équation différentielle suivante qu'on appelera (E) :
y'=0.1y (10-y)
y=(0)=1
1/ Solution approché :
Tracer dans un repere orthogonal l'approximation de la solution fournie par la méthode d'euler sur l'intervalle [0;5] en subdivisnat l'intervalle en 10 (pas : h=0.5)
Unités: 2cm sur l'axe des abscisses et 1cm sur l'axe des ordonnées.
Le tableau suivant pourra etre complété par un tableur ou à l'aide de la calculatrice :
n . 0 1 2 3 4 5 6 7 8 9 10
Xn 0
Yn 1
2/Solution exacte :
Montrer que la fonction f définie sur R par f(x) = 10 / (1+9e^(-x)) est solution de (E).
Etuider la fonction f (limites, asymptotes, sens de variation) et tracer sa représentation graphique dans le repére précédent.
:hein:
Exercice :
On considere l'équation différentielle suivante qu'on appelera (E) :
y'=0.1y (10-y)
y=(0)=1
1/ Solution approché :
Tracer dans un repere orthogonal l'approximation de la solution fournie par la méthode d'euler sur l'intervalle [0;5] en subdivisnat l'intervalle en 10 (pas : h=0.5)
Unités: 2cm sur l'axe des abscisses et 1cm sur l'axe des ordonnées.
Le tableau suivant pourra etre complété par un tableur ou à l'aide de la calculatrice :
n . 0 1 2 3 4 5 6 7 8 9 10
Xn 0
Yn 1
2/Solution exacte :
Montrer que la fonction f définie sur R par f(x) = 10 / (1+9e^(-x)) est solution de (E).
Etuider la fonction f (limites, asymptotes, sens de variation) et tracer sa représentation graphique dans le repére précédent.
Euh alors... Si je fais avec mon histoire de tangente je trouve:
n . 0
Xn 0
Yn 1
n . 1
Xn 0.5
Yn 1.5
n . 2
Xn 1
Yn 0.75
n . 3
Xn 1.5
Yn 1.125
Ma façon de faire :
équation tangente : y=f'(Xo) + (X-Xo) + f(Xo)
y= 1*(x-0)+1
=x+1
X1=0.5
Y1=X1+1=1.5
f(X1)= f'(X1)= environ 1.5
y= f'(X1)*(X-X1)+f(X1)
= 1.5(x-1.5)+1.5
= 1.5x-0.75
X2 = 1
Y2 = 0.75
etc... Alors ?
n . 0
Xn 0
Yn 1
n . 1
Xn 0.5
Yn 1.5
n . 2
Xn 1
Yn 0.75
n . 3
Xn 1.5
Yn 1.125
Ma façon de faire :
équation tangente : y=f'(Xo) + (X-Xo) + f(Xo)
y= 1*(x-0)+1
=x+1
X1=0.5
Y1=X1+1=1.5
f(X1)= f'(X1)= environ 1.5
y= f'(X1)*(X-X1)+f(X1)
= 1.5(x-1.5)+1.5
= 1.5x-0.75
X2 = 1
Y2 = 0.75
etc... Alors ?
Euh alors si je comprends un peu, on peut écrire :
f'(x) = 0.1f(x)
f(0) = 1 d'ou f'(0) = 0.1
équation tangente : y=f'(x0) (x-x0) + f(x0)
on commence :
y = 0.1(x-0) +1
=0.1x + 1
donc x1 = 0.5 et y1 = 0.1x1 + 1 = 1.05
f(x1) = 1.05
f'(x1) = 0.105
y= f'(x1) (x-x1) + f(x1)
= 0.105x - 0.525 +1.05
= 0.105x + 0.525
donc x2 = 1 et y2 = 0.105x2 + 0.525 = 0.63
f(x2) = 0.63
f'(x2) = 0.063
y= f'(x2) (x-x2) + f(x2)
= 0.063x - 0.063 . 063
= 0.063x + 0.567
donc x3 = 1.5 et y3 = 0.063x3 + 0.567 = 0.6615
et je continue comme ça... C'est ça ?
:hein: :triste: :doh:
f'(x) = 0.1f(x)
f(0) = 1 d'ou f'(0) = 0.1
équation tangente : y=f'(x0) (x-x0) + f(x0)
on commence :
y = 0.1(x-0) +1
=0.1x + 1
donc x1 = 0.5 et y1 = 0.1x1 + 1 = 1.05
f(x1) = 1.05
f'(x1) = 0.105
y= f'(x1) (x-x1) + f(x1)
= 0.105x - 0.525 +1.05
= 0.105x + 0.525
donc x2 = 1 et y2 = 0.105x2 + 0.525 = 0.63
f(x2) = 0.63
f'(x2) = 0.063
y= f'(x2) (x-x2) + f(x2)
= 0.063x - 0.063 . 063
= 0.063x + 0.567
donc x3 = 1.5 et y3 = 0.063x3 + 0.567 = 0.6615
et je continue comme ça... C'est ça ?
:hein: :triste: :doh:
Ca fait très longtemps que je n'ai pas vu cette méthode, mais il me semble qu'il faut procéder comme ça :
on sait que pour tout x,=0,1f(x)(10-f(x))) , et que f(0)=1.
, et que f(0)=1.
1ère étape : en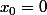 :
:
f(0)=1,=0,1.1.(10-1)=0,1.9=0,9) .
.
Equation de la tangente en 0 :
=f'(0)(x-0)+f(0)=0,9x+1) .
.
2ème étape : en :
:
on ne connaît pas) mais on connaît
mais on connaît =0,9.0,5+1=0,45+1=1,45) .
.
On calcule=0,1.g_0(0,5)(10-g_0(0,5))=0,1.1,45(10-1,45)=...) .
.
Donc=0,1.f(0,5).(10-f(0,5))\approx 0,1.g_0(0,5)(10-g_0(0,5))=t_0(0,5)) .
.
On en déduit une équation de l'approximation de la tangente en 0,5 :
=t_0(0,5)(x-0,5)+g_0(0,5)) .
.
On continue comme ça de proche en proche :
(n+1)-ième étape : en :
:
on calcule) , on calcule
, on calcule =0,1.g_{n-1}(x_n).(10-g_{n-1}(x_n))) . On en déduit
. On en déduit =t_{n-1}(x_n).(x-x_n)+g_{n-1}(x_n)) qui est une approximation de l'équation de la tangente en
qui est une approximation de l'équation de la tangente en  .
.
Compris ?
on sait que pour tout x,
1ère étape : en
f(0)=1,
Equation de la tangente en 0 :
2ème étape : en
on ne connaît pas
On calcule
Donc
On en déduit une équation de l'approximation de la tangente en 0,5 :
On continue comme ça de proche en proche :
(n+1)-ième étape : en
on calcule
Compris ?
bon voyons si j'ai compris ton explication :
x1 = 0.5
y1 = 1.45
x2 = 1
y2 = 2.07
x3 = 1.5
y3 = 2.52
x4 = 2
y4 = 3.1575
voila au moins le début, je sais qu'il existe un moyen de programmer pour faire à la calculette, est ce que quelqu'un sait comment faire pour que je puisse vérifier mes résultats et puis ça pourra me servir plus tard, j'a iune Ti-83 plus donc si quelq'un sait m'expliquer.....
x1 = 0.5
y1 = 1.45
x2 = 1
y2 = 2.07
x3 = 1.5
y3 = 2.52
x4 = 2
y4 = 3.1575
voila au moins le début, je sais qu'il existe un moyen de programmer pour faire à la calculette, est ce que quelqu'un sait comment faire pour que je puisse vérifier mes résultats et puis ça pourra me servir plus tard, j'a iune Ti-83 plus donc si quelq'un sait m'expliquer.....
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
