équation...démarche incomprise ( 2de)
21 messages
- Page 1 sur 2 - 1, 2
équation...démarche incomprise ( 2de)
Bonjour à tous !!
En fait, sur un livre de maths, j'ai cette équation :
[(3x+1)^2-4(x+3)^2]/5x^2-5 =0
On sait que le résultat est -7, mais je ne comprend pas comment faire pour trouver cette réponse ...
Quelqun peut m'aider ?
merci d'avance !
En fait, sur un livre de maths, j'ai cette équation :
[(3x+1)^2-4(x+3)^2]/5x^2-5 =0
On sait que le résultat est -7, mais je ne comprend pas comment faire pour trouver cette réponse ...
Quelqun peut m'aider ?
merci d'avance !
Pour résoudre ^2 - 4(x + 3)^2}{5 x^2-5} =0) il faut factoriser.
il faut factoriser.
Ici on doit remarquer que le numérateur est la différence de 2 carrés.
Et il faut savoir que :
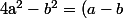(a+b))
Pour le dénominateur on met 5 en facteur et on se retrouve avec la différence de 2 carrés.
Ensuite une fraction est nulle si et seulement si son numérateur est nul, mais pas son dénominateur (ce qui ne pose pas de problème ici).
Ici on doit remarquer que le numérateur est la différence de 2 carrés.
Et il faut savoir que :
Pour le dénominateur on met 5 en facteur et on se retrouve avec la différence de 2 carrés.
Ensuite une fraction est nulle si et seulement si son numérateur est nul, mais pas son dénominateur (ce qui ne pose pas de problème ici).
Bonsoir,
Pour résoudre cette équation il faut d'abord donner un sens à son écriture (c'est faut de parler de l'ensemble de définition d'une équation, ce que enseigne quelques prof de lycée, une terminologie inéxistente en maths on la retrouve même dans les manuels de maths!!!).
Cette écriture a un sens si le dénominateur est non nul c'est à dire x est différent de -1 et de 1.
On veut dir par là que le cadre ensembliste de la résolution est IR\{-1;1}, dans ces conditions cette équation est équivalente à^2-4(x-3)^2=0)
Pour résoudre cette équation il faut d'abord donner un sens à son écriture (c'est faut de parler de l'ensemble de définition d'une équation, ce que enseigne quelques prof de lycée, une terminologie inéxistente en maths on la retrouve même dans les manuels de maths!!!).
Cette écriture a un sens si le dénominateur est non nul c'est à dire x est différent de -1 et de 1.
On veut dir par là que le cadre ensembliste de la résolution est IR\{-1;1}, dans ces conditions cette équation est équivalente à
Faudrai un peu arrêter de discuter sur le vocabulaire mathématiques et de proposer une solution x :dodo:
Figurais-vous que j'ai la solution. :id:
Supprimé par la modération - Tu devrais lire la politique du forum: si tu as la solution, tant mieux pour toi! mais le principe du forum, c'est que le demandeur trouve lui-même la solution.
Premier et dernier avertissement.
Figurais-vous que j'ai la solution. :id:
Supprimé par la modération - Tu devrais lire la politique du forum: si tu as la solution, tant mieux pour toi! mais le principe du forum, c'est que le demandeur trouve lui-même la solution.
Premier et dernier avertissement.
Geek-R a écrit:
En Latex on n'utilise pas la touche avec puissance 2 mais il est impératif d'écrir x^2. Il comprend pas x².
Donc Solutions Interdites : { 1 ; -1 }
On dit pas solutions interdites mais valeurs interdites si vous voulez.
Passons maintenant à la résolution de la fractions-produits. Une fractions est nul si et seulement si le numérateur est nul
et le dénominateur est non nul.
Donc nous devons arriver à prouver que : (3x+1)²-4(x+3)² est nul
On ne veux pas prouver que cette quantité est nulle mais on cherche les valeurs de x pourlesquelles elle est nulle.
(3x+1)²-4(x+3)²
= (3x+1)²-2²(x+3)²
= (3x+1)²-(2x+6)²
Ceci est l'une des identité remarqueables avec la différence de deux carrés.
Maintenant , l'équation-produit :
= (3x+1+2x+6)(3x+1-2x-6)
= (5x+7)(x-5)
5x+7=0 OU x-5=0
5x=-7 x= 5
x=-7/5
S={-7/5 ; 5 }
Vous pouvez vérifié la fractions de départ qu'avec x=-7/5 et x=5 le résultat est bien 0 et c'est la seul et unique solution !
Je vois nul part l'équation à résoudre dans votre rédaction!
Geek-R a écrit:Corrigé ^^
PS: solmix , si tu veux vraiment comprendre comment ca marche , essaie de voir la facon avec laquel j'ai résolu cette "fraction-produit" ( c'est moi aussi ma première fraction-produit que je resoud :zen: ) , tu verra que c'est quazi-comme une équation produit à 2 facteurs .
Fais attention à l'avertissement ci-dessus!
Cette équation quotient est définie sur
C'est une équation produit de niveau 3ème...
Je te laisse finir...
solmix a écrit:Bonjour à tous !!
En fait, sur un livre de maths, j'ai cette équation :
[(3x+1)^2-4(x+3)^2]/5x^2-5 =0
On sait que le résultat est -7, mais je ne comprend pas comment faire pour trouver cette réponse ...
Quelqun peut m'aider ?
merci d'avance !
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
