Bonjour je bloque sur une équation complexe
(z+2)^3 = 3i
Un peu d'aide serais la bienvenue
Équation complexe
7 messages
- Page 1 sur 1
Re: Équation complexe
par Ben314 » 14 Nov 2021, 13:50
Salut,
Comment calcule-t-on LES racines cubique d'un complexe ?
Comment calcule-t-on LES racines cubique d'un complexe ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Équation complexe
par azf » 14 Nov 2021, 13:54
Bonjour
On va noter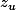
avec 
les trois solutions de votre équation ^3 = 3i)
On peut commencer par rechercher les trois solutions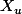
avec de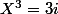 
sachant que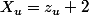 
et donc cela revient dans un premier temps à rechercher les trois racines de
Posez donc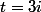
L'argument principal de
dans 
est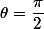 
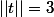
Les trois racines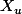 avec sont donc
+i.sin\left(\dfrac {\theta }{3}\right)\right))
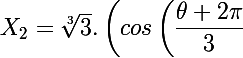+i.sin\left(\dfrac {\theta +2\pi }{3}\right)\right))
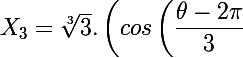+i.sin\left(\dfrac {\theta -2\pi }{3}\right)\right))
Comme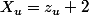 donc comme 
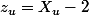alors
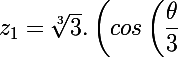+i.sin\left(\dfrac {\theta }{3}\right)\right)-2)
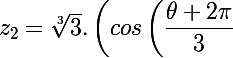+i.sin\left(\dfrac {\theta +2\pi }{3}\right)\right)-2)
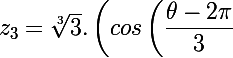+i.sin\left(\dfrac {\theta -2\pi }{3}\right)\right)-2)
On va noter
On peut commencer par rechercher les trois solutions
et donc cela revient dans un premier temps à rechercher les trois racines de
Posez donc
L'argument principal de
Les trois racines
Comme
Re: Équation complexe
par catamat » 14 Nov 2021, 14:53
Bonjour
Si on connait les racines cubiques de l'unité, 1, j et j² (ou conjugué de j) on peut trouver rapidement..
Connaissant une solution particulière notée s, les autres sont sj et sj².
Ici s=
Si on connait les racines cubiques de l'unité, 1, j et j² (ou conjugué de j) on peut trouver rapidement..
Connaissant une solution particulière notée s, les autres sont sj et sj².
Ici s=
Re: Équation complexe
par fpaco » 14 Nov 2021, 15:50
Ok merci infiniment de votre aide
C beaucoup plus claire !
Enfait je bloquais avec les racine cubiques de nombres complex car je n'en avais pas encore fait.
Merci bcp
C beaucoup plus claire !
Enfait je bloquais avec les racine cubiques de nombres complex car je n'en avais pas encore fait.
Merci bcp
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :