Equation cartésienne

[Corentin.]

Bonjour, alors voilà, je viens de commencer les équations cartésienne et j'ai du mal à comprendre.

J'ai un exercice ou je dois trouver une équation de la droite d passant par: A(-1;4) et parallèle à la droite d'equation: 3x-2y+1=0

Merci d'avance.

[mcar0nd]

Salut,

Tu as plusieurs façons de faire, tu as commencer quelque chose déjà? ;)

[Corentin.]

J'ai commencer par faire quelque chose mais sa me parais bien trop simple et rapide pour être bon..
J'ai mis comme si A(x;y) dans l'equation.

[Carpate]

Bonjour, alors voilà, je viens de commencer les équations cartésienne et j'ai du mal à comprendre.

J'ai un exercice ou je dois trouver une équation de la droite d passant par: A(-1;4) et parallèle à la droite d'equation: 3x-2y+1=0

Merci d'avance.

Une équation réduite sera donc :
Il faut que tu exprimes :
- que cette droite passe par
- qu'elle est parallèle à la droite d'équation:
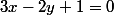
Que peut-on dire des coefficients directeurs de 2 droites parallèles ?

[mcar0nd]

J'ai commencer par faire quelque chose mais sa me parais bien trop simple et rapide pour être bon..
J'ai mis comme si A(x;y) dans l'equation.

Tu verras, c'est tout simple.

L'équation cartésienne que tu cherches, tu connais déjà pas mal de truc sur elle, tu n'as plus qu'à chercher c en fait.
Bah c'est juste, tu remplace, dans ton équation, x par l'abscisse de A et y par l'ordonnée de A.

[Corentin.]

Une équation réduite sera donc :
Il faut que tu exprimes :
- que cette droite passe par
- qu'elle est parallèle à la droite d'équation:
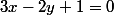
Que peut-on dire des coefficients directeurs de 2 droites parallèles ?

y=mx+p alors 4= m(-1)+p ?

Les coefficients directeurs de 2 droites parallèles ont le même vecteur directeur non ?

[mcar0nd]

y=mx+p alors 4= m(-1)+p ?

Les coefficients directeurs de 2 droites parallèles ont le même vecteur directeur non ?

Oui, deux droites parallèles ont le même coefficient directeur.

[Corentin.]

y=mx+p alors 4= m(-1)+p ?

[mcar0nd]

y=mx+p alors 4= m(-1)+p ?

Oui, mais que vaut le coefficient directeur de la droite d'équation d'équation ?

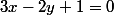
[Carpate]

Oui, mais que vaut le coefficient directeur de la droite d'équation d'équation ?

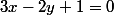
Il faut la mettre sous la forme d'équation réduite et alors le coefficient directeur est le coefficient de x

[mcar0nd]

Il faut la mettre sous la forme d'équation réduite et alors le coefficient directeur est le coefficient de x

Oui oui je sais mais je lui posais la question.

[Carpate]

Oui oui je sais mais je lui posais la question.

Ah, excuse, je m'étais trompé d'interlocuteur !

[Corentin.]

Le coefficient directeur est 3 ?

[mcar0nd]

Ah, excuse, je m'étais trompé d'interlocuteur !

C'est pas grave.

Le coefficient directeur est 3 ?

Hum non, si tu pars de ton équation cartésienne et que tu veux obtenir la forme réduite, c'est à dire de la forme , tu obtiens quoi?

[Carpate]

Le coefficient directeur est 3 ?

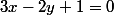
Non, tu n'as pas mis sous forme d'équation réduite ...

[Corentin.]

Ah, le "m" et le "p" sont le "a" et le "b" de l'équation cartésienne ? Donc y=3x-2 ?

[mcar0nd]

Ah, le "m" et le "p" sont le "a" et le "b" de l'équation cartésienne ? Donc y=3x-2 ?

Non, fait étape par étape.
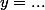
Par de l'équation cartésienne et transforme là pour que tu trouves à la fin.

[Carpate]

Ah, le "m" et le "p" sont le "a" et le "b" de l'équation cartésienne ? Donc y=3x-2 ?

C'est des calculs de 4ème !

[Corentin.]

La première étape, je fais quoi, je n'arrive pas trop a comprendre...

[mcar0nd]

Maintenant que tu as l'équation réduite de la première équation, exprime l'équation que tu cherche en fonction de cette première équation réduite et des du point A. ;)