Equation bizarre...

par **Hardtoexplain91** » 07 Déc 2007, 21:19

bonsoir; je n'arrive pas à résoudre ces deux équations pourtant j'en ai fait beaucoup..:

sinx+cosx=-1

ici, cela me donne cosx(cosx+1)+sinx(sinx+1)=0
mais je vois pas comment on pourrait la résoudre

sinx+cosx=racine2

là non plus...

Je n'y arrive pas aussi pour celle là, par contre c'est une inéquation:

Dans [0,2pi[,

1/2=< sinx<=racine3/2
-racine2/2

Je n'ai jamais vu ce genre d'équa(inéqua)tions...

Peut-être que je ne vois rien, mais bon :s

par **raito123** » 07 Déc 2007, 21:22

J'ai rien piger à ton résonnement? :hein:

par **Hardtoexplain91** » 07 Déc 2007, 21:24

Bah, faut résoudre ces équations et inéquations

mais je ne vois pas comment

par **raito123** » 07 Déc 2007, 21:32

ici, cela me donne cosx(cosx+1)+sinx(sinx+1)=0

?????.
je préfére poser

donc on obtient

puis changement de variable

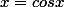
facile celle là? non

par **Hardtoexplain91** » 07 Déc 2007, 21:34

comment arrivezvous del 'équation à cosx= racine(2cos²x+1)?
j'ai pa scompris votre changement de variable...

par **Sa Majesté** » 07 Déc 2007, 21:37

Pour résoudre
a cosx + b sinx = c
on peut diviser par d = racine (a²+b²), en supposant (a,b) différent de (0,0)
a/d cosx + b/d sinx = c/d

On pose t tel que
cos t = a/d
sin t = b/d
(on a bien cos²t + sin²t = 1)
t est défini modulo 2pi

On a alors
cost cosx + sint sinx = c/d
cos(x-t) = c/d

Si |c/d| > 1 alors pas de solution
Sinon on pose u tel que
cosu = c/d

cos(x-t)=cosu
x-t=+ou- u modulo 2pi
x=t +ou- u modulo 2pi

par **Hardtoexplain91** » 07 Déc 2007, 21:43

euh, j'ai pas tout compris. Vous n'auriez pas une autre solution? psk enfin, normalement, je ne sais pas que acos+.....=c

par **Sa Majesté** » 07 Déc 2007, 21:50

C'est pourtant simple :
sinx+cosx=-1
racine(2)/2 sinx + racine(2/2) cosx = -racine(2)/2
sin(pi/4) sinx + cos(pi/4) cosx = cos(3pi/4)
cos(x-pi/4)=cos(3pi/4)
x-pi/4=3pi/4 + 2k pi ou x-pi/4=-3pi/4 + 2k pi
x=pi + 2k pi ou x=-pi/2 + 2k pi
x=(2k+1) pi ou x=-pi/2 + 2k pi

par **Hardtoexplain91** » 07 Déc 2007, 22:16

Ah daccord!
ok merci ^^. En appliquant cela dans ]-pi,pi], les solutions sont bien pi et -pi/2 ou y a- til d'autre solutions svp?

par contre, pour l'inéquation auriez-vous une idée?
1/2=< sinx<=racine3/2

par **sisu88** » 07 Déc 2007, 22:28

C'est pas dure ça!! Tu saus que sin(pi/3)=V3/2 et que sin(pi/6)=1/2
Donc, Pi/6=
La trigo c'est un des seuls truc que j'arrive à peu près à maitriser cette année lool Dure dure la 1ère S

par **Hardtoexplain91** » 08 Déc 2007, 15:06

c'est la même méthode pour sinx+cosx=racine2?

jtrouve un truc bizarre o_o

par **Hardtoexplain91** » 08 Déc 2007, 15:29

Quelquun pourrait til mexpliquer le principe des intervalles car je ne suis jamais sure.

Pour les deux dernieres inéquations,
pour 1/2=
mais on précise sur [0,2pi[, est-ce bon ce que j'a itrouvé?

par **Hardtoexplain91** » 08 Déc 2007, 15:33

J'ai essayé d'en faire une autre sur [0,2pi[, pour voir...

l'inéquation est celle-ci: -racine2/2
Je trouve S[0,2pi[= ]3pi/4,4pi/3]U]7pi/4,pi/3]

Mais sont-ce les résultats de [0,2pi[ ?

De plus, pour

sinx+cosx=racine2
En appliquant votre méthode, j'ai racine2/2sinx+racine2/2cosx= 1
je dis que cos(pi-pi/2)=1 ou autre chose...?

par **Hardtoexplain91** » 08 Déc 2007, 15:35

Dsl, encore une autre question, ...
Sinteta >=costeta , ssi teta appartient à ]-pi/4, 5pi/4[.
l'énoncé s'est trompé non? Il faudrait que sinteta>costeta et pas égal.. ?
Car sinteta=costeta ssi x=-pi/4 ou 5pi/4

par **raito123** » 08 Déc 2007, 18:27

Hardtoexplain91 a écrit:Dsl, encore une autre question, ...
Sinteta >=costeta , ssi teta appartient à ]-pi/4, 5pi/4[.
l'énoncé s'est trompé non? Il faudrait que sinteta>costeta et pas égal.. ?
Car sinteta=costeta ssi x=-pi/4 ou 5pi/4

T'es sûr de ton énoncé?et aussi t'es sûr de ce que tu dit?

par **Hardtoexplain91** » 08 Déc 2007, 18:34

l'énoncé est tel que :

sinteta>=costeta ssi teta appartient ]pi/4, 5pi/4[

Faut montrer ça.
Mais moi je pensais que l'énoncé s'était trompé et que c'était plutôt:

sinteta>costeta ssi teta appartient ]pi/4, 5pi/4[

Sinon, pouvez vous m'aider pour les équations svp...... et me dire le principe des intervalles

par **raito123** » 08 Déc 2007, 18:36

u sais que tu as mis en haut un moins'-'et pas en ton dernier post

par **Hardtoexplain91** » 08 Déc 2007, 18:42

Dsl! j'ai mal vu alors c'est bien pi/4

par **Sa Majesté** » 08 Déc 2007, 18:48

Avec la même méthode
sinx+cosx=racine2
racine(2)/2 sinx + racine(2/2) cosx = 1
sin(pi/4) sinx + cos(pi/4) cosx = cos(0)
cos(x-pi/4)=cos(0)
x-pi/4=0 + 2k pi
x=pi/4 + 2k pi

par **Hardtoexplain91** » 08 Déc 2007, 18:58

ah d'accord, je bloquais justement sur le fait que cosx=0, jcroyais que c'était interdit t_t...

pourriez-vous répondre à mes questions précédentes svp?

merci bcp :)

Equation bizarre...

Equation bizarre...

Qui est en ligne