équation avec coeff binomiaux
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 01 Fév 2015, 09:31
par t.itou29 » 01 Fév 2015, 09:31
Bonjour,
Je cherche à résoudre l'équation :
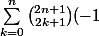^k\times x^{2k+1}=0)
En considérant le développement de
x))
Pour le dvpmt j'ai trouvé:
x)=\sum_{k=0}^n \binom{2n+1}{2k+1}(-1)^k\times cos^{2(n-k)}(x)\times sin^{2k+1}(x))
Après je pensais faire un chgt de variable mais ce n'est pas possible directement, faudrait que j'arrive à me débarrasser du cos mais je vois pas comment...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Fév 2015, 13:18
par zygomatique » 01 Fév 2015, 13:18
salut
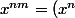^m)

...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 02 Fév 2015, 18:51
par t.itou29 » 02 Fév 2015, 18:51
zygomatique a écrit:salut
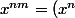^m)

...
Ça donnerait
^{n-k}*sin^{2k+1}(x))
mais le problème est que l'équation de départ (en testant avec n=2,3) admet des solutions non comprise dans [-1;1], et en plus je ne sais pas comment me ramener à l'équation de départ

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Fév 2015, 21:22
par zygomatique » 02 Fév 2015, 21:22
2(n - k) = 2n - 2k = 2n +1 - (2k + 1)
et
2n + 1 - (2k + 1) + 2k + 1) = 2n + 1
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
