équa diff avec 2nd membre

[JackeOLanterne]

L'ensemble des cas est traité dans ce cours : un exemple fourni est d'ailleurs comparable à celui-ci.

[Dinozzo13]

Salut !

Voici un petit plan de la résolution de l'équation différentielle :


1°) On détermine l'ensemble des fonctions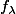 solutions de l'équation homogène : .

2°) On détermine une fonction particulière solution de l'équation .

3°) En conséquent :

Par conséquent, toutes les fonctions solutions de sont définies par :

[sad13]

En gros il te dit qu'il y a deux étapes:
1/résolution ou trouver une solution de l'équation homogène
2/trouver une solution particulière

et la solution finale ou générale n''est autre que la somme de ces deux deux solutions citées ci-dessus, c'est clair?

Quant àa la solution particulière, je croyais l'avoir trouvée mais en vain, il a y a un petit truc qui m'échappe

[sad13]

Tu te demandes la solution? BEn je ne trouve la particulière, @ tte à l'h

[Dinozzo13]

Je me questionne sur une seule étape précise de la résolution, qui est enfantine lorsqu'on connait la forme de ..... mais encore faut-il la connaitre cette forme!


pour memo


en tout cas si tu veux résoudre l'équa diff, je te conseille de postuler que est de la forme , et tu résoudras l'exo sans peine...
par contre ne me demande pas d'où je sors cette forme... c'est ce que je me désespère à comprendre
:mur:

Salut !

He bien, il faut savoir que si tu as, sur le membre de droite quelque chose de la forme :
- alors la solution particulière est de la forme où k est à déterminer ;
- : un polynôme de degré alors la solution particulière est un polynôme de même degré.*
Exemple : Imaginons que tu aies
Ta solution particulière est un polynôme de degré 7 de la forme : où les sont à déterminer ;
- Enfin, mais la c'est beaucoup plus rare au lycée, et c'est surtout guidé lors d'un exercice, si tu as alors là, il faut le savoir, on cherche une solution particulière de la forme où et sont à déterminer.

Voilà, en espérant t'avoir répondu :+++:
-