Ex eponentielles, nbrs complexes

[maths0]

[CENTER][/CENTER]

[annick]

Si le sinus est négatif, tu ne peux pas avoir pi/4.

Sinon, pour la suite de ta question, je passerai en notation exponentielle, ça permet de répondre très vite et de bien simplifier les calculs.

[droopy5782]

Ah oui
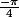
En effet c'est mieux merci :we:

[maths0]

Soit 2 nombres complexes: et , alors:
[CENTER] [/CENTER].

[droopy5782]

Soit 2 nombres complexes: et , alors:
[CENTER] [/CENTER].

Oui d'accord mais ça c'est une forme exponentielle, pas trigonométrique.

Donc la réponse à ma question est que la forme trigonométrique

=

(sans vous détailler les calculs), ça c'est la forme trigonométrique ?!

[maths0]

Oui d'accord mais ça c'est une forme exponentielle, pas trigonométrique.

Donc la réponse à ma question est que la forme trigonométrique

=

(sans vous détailler les calculs), ça c'est la forme trigonométrique ?!

Non la forme trigonométrique et la forme exponentielle sont quasi identiques.
Pour l'écrire il faut: le module et l'argument du nombre complexe.
Or ici me module de ton nombre complexe n'apparait pas !
En plus c'est complétement faux ! le nombre que tu viens d'écrire n'est pas "complexe" !

[annick]

Passe d'abord par la forme exponentielle, quitte à revenir à la forme trigonométrique au final.

[droopy5782]

Passe d'abord par la forme exponentielle, quitte à revenir à la forme trigonométrique au final.

?

[maths0]

?

Tu n'as pas lu ?

[annick]

Oui, donc e^i((2pi+3pi)/12)=e^i(5pi/12)= cos(5pi/12)+isin(5pi/12)

[annick]

Je trouve c =

Excuse-moi, mais je t'ai dit que c'était juste car je n'avais pas regardé le module. En fait, sauf erreur de ma part, le module est V2 et non V3.
Ce qui te donne bien un module de 1 pou z1/z2

[droopy5782]

Voilà j'ai fini !!
Mes résultats coïncides ^^

Merci beaucoup de m'avoir aidé, et de m'avoir aidé à comprendre mes erreurs :-)

[VincentESAIP]

peut on m'aider à trouver le module du nombre complexe suivant :

z=e^2-i

Merci de votre aide.