Ensemble vérifiant une relation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 17:48
par cuicuiman » 23 Jan 2011, 17:48
Bonsoir tout le monde.
Mon prof' nous a donné un petit exercice qui me pose quelques problèmes ! :mur:
(E) l'ensemble des points M du plan dont les coordonnées vérifient la relation
x² + y² - 2x - 6y + 8 = 0
Nature de l'ensemble (E) ?
En parcourant le web, j'en ai conclu qu'il fallait que je factorise tout ça mais je ne vois pas comment :cry:
Pourrait-on m'indiquer la marche à suivre ?
Merci d'avance

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 17:52
par Sa Majesté » 23 Jan 2011, 17:52
Salut
Il faut écrire sous forme de carrés
x² + y² - 2x - 6y + 8 = 0
(x-a)² + (y-b)² + c = 0
A toi de trouver a et b, et d'en déduire c
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:04
par cuicuiman » 23 Jan 2011, 18:04
(x-a)² + (y-b)² + c = 0 ? Jamais vu de ma vie !
Je connaissais ax + by + c = 0
ou en encore (x-a)² + (y-b)² = R²
Pourrais-tu m'expliquer ce qu'est cette relation ?
Mais bon bref, en suivant cette nouvelle formule, je trouve
(x-1)² + (y-3)² - 2 = 0
Comme je l'ai dis plus haut, je calcule mais je ne comprends pas !
A quoi tout ça correspond ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:11
par Sa Majesté » 23 Jan 2011, 18:11
cuicuiman a écrit:Mais bon bref, en suivant cette nouvelle formule, je trouve
(x-1)² + (y-3)² - 2 = 0
Comme je l'ai dis plus haut, je calcule mais je ne comprends pas !
A quoi tout ça correspond ?
OK
Alors maintenant appelons C le point de coordonnées (1;3)
A quoi correspond (x-1)² + (y-3)² ?
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:16
par cuicuiman » 23 Jan 2011, 18:16
Huummm....
Un de ces fameux points vérifiant l'équation ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:19
par Sa Majesté » 23 Jan 2011, 18:19
Non
Soit M(x;y) un point de (E)
alors x et y vérifient (x-1)² + (y-3)² = 2
Maintenant soit C(1;3)
A quoi correspond (x-1)² + (y-3)² ?
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:23
par cuicuiman » 23 Jan 2011, 18:23
On utilise les coordonnées de C ( 1 ; 3)
... ce qui donne 0 !
Mais bon, on se retrouve avec 0 = 2
Plutot incohérent !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:26
par Sa Majesté » 23 Jan 2011, 18:26
Bon là tu racontes carrément n'imp !
Qui a dit que C est dans (E) ?
Et of course il ne l'est pas puisque qd tu remplaces x par 1 et y par 3, l'équation n'est pas vérifiée
Quelles sont les coordonnées de
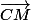
?
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:28
par cuicuiman » 23 Jan 2011, 18:28
Coordonnées du vecteur CM
CM (x-1 : y-3)
désolé, je ne sais pas faire le signe vecteur

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:31
par Sa Majesté » 23 Jan 2011, 18:31
cuicuiman a écrit:désolé, je ne sais pas faire le signe vecteur
Pas grave :lol3:
cuicuiman a écrit:Coordonnées du vecteur CM
CM (x-1 : y-3)
Oui et donc à quoi correspond (x-1)² + (y-3)² ?
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:36
par cuicuiman » 23 Jan 2011, 18:36
Le carré de sa norme ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:37
par Sa Majesté » 23 Jan 2011, 18:37
cuicuiman a écrit:Le carré de sa norme ?
:++:
Oui (x-1)² + (y-3)² = CM²
donc tu aboutis à CM² = 2
Donc où se trouve M ?
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:40
par cuicuiman » 23 Jan 2011, 18:40
Eloigné de 2 unités par rapport à C !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:42
par Sa Majesté » 23 Jan 2011, 18:42
Pas tout à fait : éloigné de

car
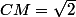
Quel est l'ensemble des points éloignés d'une valeur fixe d'un point fixe ?
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:43
par cuicuiman » 23 Jan 2011, 18:43
Un cerle :zen:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:48
par Sa Majesté » 23 Jan 2011, 18:48
Yes !
Et même plus précisément LE cercle de centre C et de rayon

Maintenant en toute rigueur tu as montré que (E) est inclus dans le cercle
Il faudrait faire la réciproque c'est-à-dire montrer que le cercle est inclus dans (E) pour montrer que (E) est égal au cercle
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 18:52
par cuicuiman » 23 Jan 2011, 18:52
Oula ! Et comment je démontre ça ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:57
par Sa Majesté » 23 Jan 2011, 18:57
Je ne suis pas absolument certain que ça soit nécessaire car ici on peut dire
M appartient à (E) ssi x² + y² - 2x - 6y + 8 = 0 ssi (x-1)² + (y-3)² = 2 ssi CM = racine(2)
Qd on arrive à utiliser des "ssi" partout alors il n'y a pas de pb
Sinon il faut démontrer la réciproque
Tu prends un point M(x;y) sur le cercle
Alors CM = racine(2) donc (x-1)² + (y-3)² = 2 donc x² + y² - 2x - 6y + 8 = 0 donc M appartient à (E)
Et c'est fini !
-
cuicuiman
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Déc 2010, 21:55
-
 par cuicuiman » 23 Jan 2011, 19:00
par cuicuiman » 23 Jan 2011, 19:00
Et dernière petite chose.
Peux-tu m'expliquer la formule de tout à l'heure :
(x-a)² + (y-b)² + c = 0
Car comme je te l'ai dis, je ne l'ai jamais vu !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 19:04
par Sa Majesté » 23 Jan 2011, 19:04
Hmmm ... que veux-tu que j'explique ?
En fait c'est un grand classique : quand tu as x² + y² + Ax +By + C = 0, tu essaies de le mettre sous la forme (x-a)² + (y-b)² + c = 0, comme tu l'as très bien fait, pour trouver l'ensemble cherché
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
