Ensemble de dérivabilité d'une fontion composé d'un ln(x) :

[ddiudu]

Bonjour,

je dois déterminer l'ensemble de dérivabilié de


f(x)=ln(x-7)*5+1/ln(x)- (5+ln(x^2))/(8+x)


je ne sais pas trop comment m'y prendre...


Commnt dois je faire :

dériver puis faire comme pour la détermination de l'ensemble de définition d'une fonction avec un ln(A) [quand A est positif quoi...].


Merci par avance pour vos réponses,

[zygomatique]

salut

il suffit de répondre à ces deux questions ::

à quelle condition un quotient existe ?

à quelle condition peut-on prendre le logarithme d'un nombre ?

[ddiudu]

salut

il suffit de répondre à ces deux questions ::

à quelle condition un quotient existe ?

à quelle condition peut-on prendre le logarithme d'un nombre ?

mais ça c'est pour l'ensemble de définiion ; pas de dérivabilité non ?

[capitaine nuggets]

On a le résultat suivant :

Soit une fonction définie de domaine de définition .
Alors on peut dire en quelque sorte que est au moins dérivable sur privé de ses éventuelles bornes.

Cas récurrent du lycée : si s'écrit comme réunion d'intervalle(s), alors est au moins dérivable sur la réunion de ces même intervalles mais ouverts .

Par exemple, si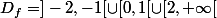 alors tu peux directement affirmé que est dérivable sur .
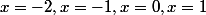Pour évaluer la dérivabilité de en et 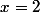, il faut passer par la définition de la dérivabilité d'une fonction.

Un exemple classique est la fonction racine carrée définie sur . On peut d'ores et déjà affirmer qu'elle est dérivable sur l'intervalle ouvert correspondant . Mais elle n'est pas dérivable sur , car pas dérivable en (montrer que la limite du taux d'accroissement n'est pas finie).

Après il faut faire attention et regarder comment est définie. Par exemple la valeur absolue est bien définie sur , mais n'est dérivable que sur 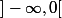et sur 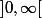(donc pas en 0).
Cela vient du fait que pour tout réel, 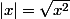, ou encore que l'on peut la définir par morceaux :

[CENTER]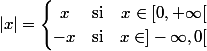[/CENTER]



:+++:

[chombier]

On a le résultat suivant :

Soit une fonction définie de domaine de définition .
Alors on peut dire en quelque sorte que est au moins dérivable sur privé de ses éventuelles bornes.

(...)

Après il faut faire attention et regarder comment est définie. Par exemple la valeur absolue est bien définie sur , mais n'est dérivable que sur et sur (donc pas en 0).
Cela vient du fait que pour tout réel, , ou encore que l'on peut la définir par morceaux :

[CENTER][/CENTER]



:+++:

C'est très bizarre, ta théorie, elle serait juste pour tout fonction sauf si on peut la définir par morceaux ? Mais tout fonction peut être définie par morceaux, ça ne m'a pas l'air très scientifique...

Apres il est vrai que la PLUPART des fonction en lycée sont définies comme somme, produit, quotient et composition et qu'elles sont LE PLUS SOUVENT dérivables sur leur ensemble de définition.

Un cas particulier est celui de la racine carrée : par exemple la fonction .

Elle est définie partout où u est positive ou nulle.
Elle est dérivable partout où u est strictement positive.
Sur les points où u s'annule, on ne peut rien dire a priori...

[chombier]

Pour le problème de départ :

Elle est typiquement obtenue par somme, produit, quotient et composition de fonctions dérivables sur leur ensemble de définition.

Elle est donc dérivable sur son ensemble de définition :zen: