Enigme mathematique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 22 Oct 2009, 15:22
par and1dx » 22 Oct 2009, 15:22
Bonjour,
J'ai une enigme a vous proposé:
Dans un carre de 10 "petits" carreaux" sur 10 "petits carreaux", combien de rectangles peut ont faire ?
Pour corser le tous on demande uniquement des rectangles et pas de carrés !!!!
A vous je jouer ;)
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 22 Oct 2009, 15:26
par and1dx » 22 Oct 2009, 15:26
je trouve pour ne pas donne la reponse entre 2000 et 3000
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 22 Oct 2009, 15:27
par Timothé Lefebvre » 22 Oct 2009, 15:27
Oh, la réponse ne m'intéresse pas vraiment en fait ;)
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 22 Oct 2009, 16:32
par and1dx » 22 Oct 2009, 16:32
Alors personnes ne trouve ?
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 22 Oct 2009, 17:01
par and1dx » 22 Oct 2009, 17:01
????????????????????????????
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 22 Oct 2009, 17:30
par beagle » 22 Oct 2009, 17:30
0+2+4=6 donc 2640 ?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 22 Oct 2009, 18:01
par and1dx » 22 Oct 2009, 18:01
explique ton raisonnement ?
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 22 Oct 2009, 18:48
par and1dx » 22 Oct 2009, 18:48
???????????
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 22 Oct 2009, 18:52
par beagle » 22 Oct 2009, 18:52
désolé, je suis un peu blagueur,
mais je les ai tous ou trop ou bien il m'en manque?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 26 Oct 2009, 18:18
par and1dx » 26 Oct 2009, 18:18
oui il me semble que c'est ca tu expliquer ton raisonnement ^^ :p
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 26 Oct 2009, 18:40
par beagle » 26 Oct 2009, 18:40
pour un rectangle de kxk', k' hauteur sur verticale des colonnes, k sur horizontale des rangées,
sur les rangées je peux caser 10-(k-1) rectangles différents
sur les colonnes je peux caser 10-(k'-1)
j'ai donc [10-(k'-1)]*[10-(k-1)]
Pour un k donné j'ai tous les k' de 1 à 10,...
...donc 55x55=3025
et ensuite j'ai enlevé les carrés
j'ai eu quelques hésitations parce qu'au départ je suis parti sur une autre méthode et le nombre de rectangles devait ètre pair, et fallait faire gaffe aux carrés que l'on risquait de compter deux fois.
mème maintenant je ne suis pas sur du résultat
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Oct 2009, 18:46
par benekire2 » 26 Oct 2009, 18:46
LOL c'est sur c'est hyper utile comme truc!!
Cas général: Combien y a-il de rectangles dans un carré de coté n ?
-
and1dx
- Membre Naturel
- Messages: 90
- Enregistré le: 15 Oct 2008, 16:03
-
 par and1dx » 26 Oct 2009, 19:50
par and1dx » 26 Oct 2009, 19:50
Cas general pour un carre de cote n:
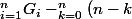^2)
oû
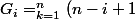(n-k+1))
Bien sure elle doit se simplifier mais c'est comme ca que moi j'ai trouve ^^
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Oct 2009, 19:57
par benekire2 » 26 Oct 2009, 19:57
Je ne suis malheureusement pas expert en somme ( Timothé pourra bien te le confirmé!! )
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 26 Oct 2009, 20:00
par Timothé Lefebvre » 26 Oct 2009, 20:00
Ah bah j'allais dire justement qu'on allait t'attendre ^^
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Oct 2009, 20:10
par benekire2 » 26 Oct 2009, 20:10
A toi l'honneur tim!! C'est ceductible cette bête au moins?
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 26 Oct 2009, 20:20
par beagle » 26 Oct 2009, 20:20
55x55 était le carré de: n*(n+1)/2
avec n= 10
(pour les rectangles avec les carrés qui sont des rectangles réguliers.)
cela marche avec 0, 1 ,2
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 26 Oct 2009, 20:33
par beagle » 26 Oct 2009, 20:33
la somme des carrés consécutifs serait n(n+1)(2n+1)/6
ce qui pour n=10 semble marcher cela faisait 385
donc rectangles sans les carrés:
n(n+1)/2 au carré - n(n+1)(2n+1)/6
donc ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
