Enigme des caméléons
26 messages
- Page 1 sur 2 - 1, 2
Enigme des caméléons
Bonjour,
Je dois faire un devoir maison pendant les vacances mais là je suis bloqué au point mort, je tiens a préciser au cas ou mon prof de maths passerait par là, que je poste ici sans penser à une quelconque tricherie. Je pense qu'on peut se faire aider pour un DM. (J'espère que c'est le cas :p)
Voici :
Il y a 42 caméléons bleus, 17 rouges, 31 verts. A chaque recontre si les deux caméléons sont identiques, ils gardent leurs couleurs, sinon ils prennent la troisième (un rouge et un vert se rencontrent --> paf ils deviennent bleus) Est-ce possible que les camélons deviennent tous de la même couleurs ?
Il y a une indication : "on peut poser b0 = 42; ro=13; v0=31, on designe alors par bn, rn, et vn le nombrede caméléons de chaque couleur après la n-ième rencontre. Considerer alors la suite Un = bn-rn. on cherche les valeurss de Un modulo 3.
voilà mon soucis, les rencontrent se font aléatoirement comment est-ce possible de determiner les suites ? J'y ai réfléchi mais la je ne comprends pas. Il semple que Rn+Bn+Vn = une constante non ? (42+13+31 = 86 non ?)
Merci de votre aide je suis perdu...
(nous sommes sur le chapitre des congruences)
Je dois faire un devoir maison pendant les vacances mais là je suis bloqué au point mort, je tiens a préciser au cas ou mon prof de maths passerait par là, que je poste ici sans penser à une quelconque tricherie. Je pense qu'on peut se faire aider pour un DM. (J'espère que c'est le cas :p)
Voici :
Il y a 42 caméléons bleus, 17 rouges, 31 verts. A chaque recontre si les deux caméléons sont identiques, ils gardent leurs couleurs, sinon ils prennent la troisième (un rouge et un vert se rencontrent --> paf ils deviennent bleus) Est-ce possible que les camélons deviennent tous de la même couleurs ?
Il y a une indication : "on peut poser b0 = 42; ro=13; v0=31, on designe alors par bn, rn, et vn le nombrede caméléons de chaque couleur après la n-ième rencontre. Considerer alors la suite Un = bn-rn. on cherche les valeurss de Un modulo 3.
voilà mon soucis, les rencontrent se font aléatoirement comment est-ce possible de determiner les suites ? J'y ai réfléchi mais la je ne comprends pas. Il semple que Rn+Bn+Vn = une constante non ? (42+13+31 = 86 non ?)
Merci de votre aide je suis perdu...
(nous sommes sur le chapitre des congruences)
A chaque fois j'oublie que le nombre de caméléons est constant, je crois que lors d'une rencontre il en ressort un seul - -
Dans ce cas ça a l'air simple avec le module 3.
Si l'âge des caméléons dépend de leur couleur, et que les bleus ont un an, les rouges deux ans, et les verts trois, alors la somme des âges des caméléons avant leur rencontre et après sont congrus au même nombre modulo 3.
Si on veut qu'ils aient tous un deux ou trois ans, dans les trois cas on a la somme des âges totale multiple de trois: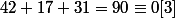
Il suffit de voir si parmis ces six nombres: (qui correspondent aux différentes combinaisons des âges)
+3(31))
+2(31))
+17+3(31))
+3(17)+31)
+17+2(31))
+2(17)+31)
Un au moins est divisible par trois, s'il n'y en a pas c'est que ce n'est pas possible que tous les caméléons aient la même couleur.
Dans ce cas ça a l'air simple avec le module 3.
Si l'âge des caméléons dépend de leur couleur, et que les bleus ont un an, les rouges deux ans, et les verts trois, alors la somme des âges des caméléons avant leur rencontre et après sont congrus au même nombre modulo 3.
Si on veut qu'ils aient tous un deux ou trois ans, dans les trois cas on a la somme des âges totale multiple de trois:
Il suffit de voir si parmis ces six nombres: (qui correspondent aux différentes combinaisons des âges)
Un au moins est divisible par trois, s'il n'y en a pas c'est que ce n'est pas possible que tous les caméléons aient la même couleur.
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
