Encore une suite qui me pose probleme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 29 Déc 2009, 02:15
par newton » 29 Déc 2009, 02:15
OUPS je voulais parler de limites
soit f fx 2x^3-5x²-x+6/x²-3x+2 df R-(1,2)
1- factoriser P=2x^3-5x²-x+6
voila voiou (x-2)(x+1)(2x-3)
(x-2)(x+1)(2x-3)/(x-1)(x-2)
2-etudier la limite de f en 2
lim x->2 f=0
(x-2)(x+1)(2x-3)/x²-3x+2
3-etudier la limite de f en -oo
lim x->-oo f=-oo/+oo=+-oo et la ????
-
sniperamine
- Membre Relatif
- Messages: 366
- Enregistré le: 19 Jan 2009, 03:46
-
 par sniperamine » 29 Déc 2009, 02:41
par sniperamine » 29 Déc 2009, 02:41
newton a écrit:OUPS je voulais parler de limites
soit f fx 2x^3-5x²-x+6/x²-3x+2 df R-(1,2)
1- factoriser P=2x^3-5x²-x+6
voila voiou (x-2)(x+1)(2x-3)
(x-2)(x+1)(2x-3)/(x-1)(x-2)
2-etudier la limite de f en 2
lim x->2 f=0
(x-2)(x+1)(2x-3)/x²-3x+2
3-etudier la limite de f en -oo
lim x->-oo f=-oo/+oo=+-oo et la ????
limf=2x^3/x²=-oo
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2009, 03:29
par Dinozzo13 » 29 Déc 2009, 03:29
tu nous dis que
=\frac{2x^3-5x^2-x+6}{x^2-3x+2})
,

1°) Puis tu as fait :
=2x^3-5x^2-x+6=(x-2)(x+1)(2x-3))
Et donc
=\frac{(x-2)(x+1)(2x-3)}{(x-1)(x-2)})
Mais, tu remarque que pour tout

de
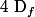
:
=\frac{(x+1)(2x-3)}{x-1})
. Tu en déduis donc :
2°)
=f(2))
3°)
)
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 29 Déc 2009, 12:32
par newton » 29 Déc 2009, 12:32
oui j avais vu mais j avais mal calcule f(x)=\frac{(x+1)(2x-3)}{x-1}.
2°) 4$ \lim_{x \to 2}f(x)=3
3°) 4$ \lim_{x \to - \infty}f(x)=+infty/-infty=+- infty je seche parceque mes cours me donne pr le quotient de ce style +-infty
PS je pensais que ca allait bien ecrire !!!!
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Déc 2009, 13:41
par Dinozzo13 » 29 Déc 2009, 13:41
:ptdr: sélectionne ton teste puis choisis la balise TEX juste au-dessus
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 29 Déc 2009, 14:09
par newton » 29 Déc 2009, 14:09
oui j avais vu mais j avais mal calcule
=\frac{(x+1)(2x-3)}{x-1}.)
2°)
=3)
3°)
=\infty/-\infty=+- \infty)
je seche parceque mes cours me donne pr le quotient de ce style +-

et je ne vois pas comment lever l indeterminé je vois pas comment factoriser ou autrement (derivé encadrement j en sais rien)
-
Blader
- Messages: 1
- Enregistré le: 31 Déc 2009, 22:32
-
 par Blader » 31 Déc 2009, 22:37
par Blader » 31 Déc 2009, 22:37
pour la 3 tu appliques la règle suivante:
en +oo ou -oo, toute fonction rationnelle a même limite que le quotient simplifié des termes de plus haut degré au numérateur et au dénominateur
Dans ce cas, tu dois donc juste étudié la lim2x en -oo :we:
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 01 Jan 2010, 10:34
par newton » 01 Jan 2010, 10:34
ok merci
je m en souviendrai
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 01 Jan 2010, 14:41
par Le_chat » 01 Jan 2010, 14:41
Dinozzo13 a écrit: Tu en déduis donc :
2°)
=f(2))
Si on regarde bien Df, on voit que f(2) n'est pas défini...
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 01 Jan 2010, 16:02
par newton » 01 Jan 2010, 16:02
Citation:
Posté par Dinozzo13
Tu en déduis donc :
2°)
=f(2))
Si on regarde bien Df, on voit que f(2) n'est pas défini...
effectivement donc on en deduis la proposition de dinozzo a chaque fois
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
