Encore et toujours ces nombres complexes ^^
61 messages
- Page 3 sur 4 - 1, 2, 3, 4
bon, pour l'instant, je vais résumer ce qui a été fait précédement.
Je veux déterminer l'ensemble des points M d'affixe z tel que
Voilà ce que j'ai fait jusque là :
Pour tout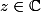 :
:\\<br />|z-i|=|z-iz| (2)<br />\end{array}<br />\right)
Je résous) :
:

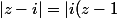|)


Soient et
et 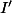 les points d'affixes respectives
les points d'affixes respectives  et
et  , par conséquent, pour tout complexe
, par conséquent, pour tout complexe  :
:



Donc l'ensemble des points
des points  du plan complexe est la médiatrice du segment
du plan complexe est la médiatrice du segment 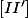 .
.
Je résous) :
:

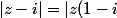|)


Et donc, pour tout :
:




^2-2(\vec{OG}+\vec{GM})^2=0)
=0)

=0)
Soit le barycentre de
le barycentre de ) et
et ) , on a donc par définition :
, on a donc par définition :

Et par conséquent :

De plus : équivaut à
équivaut à  et
et  donc :
donc :

Or donc
donc  et donc l'ensemble des points M du plan complexe est le cercle de centre G et de rayon
et donc l'ensemble des points M du plan complexe est le cercle de centre G et de rayon  .
.
Voilà pour l'instant, tout est bon jusque là ?
Je veux déterminer l'ensemble des points M d'affixe z tel que
Voilà ce que j'ai fait jusque là :
Pour tout
Je résous
Soient
Donc l'ensemble
Je résous
Et donc, pour tout
Soit
Et par conséquent :
De plus :
Or
Voilà pour l'instant, tout est bon jusque là ?
Pour ton avant dernier post #40 : c'est impec à deux détails prés :
1) Quand tu introduit G dans les calculs, écrit à coté "où G est un point que l'on choisira ultérieurement" : ça fait classe.
2) Dans la fin de la rédaction, tu ne devrait pas mettre des "donc" qui veulent normalement dire des implication. Comme tu raisonne par équivalence, ce serait mieux d'écrire "l'équation s'écrit alors" ou "ce qui équivaut à" ou "on peut réécrire l'équation sous la forme"...
(je pense qu'il faut commencer à faire la différence entre implication et équivalence)
Pour ton dernier post, la réponse est non : un système (linéaire) de deux équation à deux inconnues a une seule solution (ou bien 0 ou bien une infinité) mais jamais 2 solutions car, géométriquement, il correspond à l'intersection de deux droites.
A ton niveau, tu ne connait (presque) qu'une seule 'chose' qui produit 2 solutions...
1) Quand tu introduit G dans les calculs, écrit à coté "où G est un point que l'on choisira ultérieurement" : ça fait classe.
2) Dans la fin de la rédaction, tu ne devrait pas mettre des "donc" qui veulent normalement dire des implication. Comme tu raisonne par équivalence, ce serait mieux d'écrire "l'équation s'écrit alors" ou "ce qui équivaut à" ou "on peut réécrire l'équation sous la forme"...
(je pense qu'il faut commencer à faire la différence entre implication et équivalence)
Pour ton dernier post, la réponse est non : un système (linéaire) de deux équation à deux inconnues a une seule solution (ou bien 0 ou bien une infinité) mais jamais 2 solutions car, géométriquement, il correspond à l'intersection de deux droites.
A ton niveau, tu ne connait (presque) qu'une seule 'chose' qui produit 2 solutions...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Lire le post #38....
Je te conseillerais plutôt la méthode 'z=x+iy' car j'ai peur que tu galère un peu pour trouver l'équation de la médiatrice du segment [I'I], puis les coordonnées de G et l'équation du cercle de centre G...
Si tu as du temps, tu peut évidement faire les deux pour voir que l'on tombe trés rapidement sur le même système (non linéaire).
Je te conseillerais plutôt la méthode 'z=x+iy' car j'ai peur que tu galère un peu pour trouver l'équation de la médiatrice du segment [I'I], puis les coordonnées de G et l'équation du cercle de centre G...
Si tu as du temps, tu peut évidement faire les deux pour voir que l'on tombe trés rapidement sur le même système (non linéaire).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben ton exercice est déjà fini là, il reste plus qu'à résoudre le système à priori (enfin j'ai pas tout lu mais je crois bien que tu en es arrivé à ce stade là).
Passer par les inversions permet de voir pourquoi en partant de l'égalité sur les modules on arrive à ce système là. C'est grâce aux propriété de conservations globale de l'ensemble des droites et cercles du plan.
Passer par les inversions permet de voir pourquoi en partant de l'égalité sur les modules on arrive à ce système là. C'est grâce aux propriété de conservations globale de l'ensemble des droites et cercles du plan.
61 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
