Encore et toujours ces nombres complexes ^^
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2009, 16:23
par Ben314 » 19 Déc 2009, 16:23
Dinozzo13 a écrit:Ah, on nomme G barycentre de (I;1) et (O;2)
Oui
: donc

non ?
Non (qu'est ce que le point M vient faire ici ????)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Déc 2009, 16:50
par Dinozzo13 » 19 Déc 2009, 16:50
oups, je voulais en fait parler d'un point quelconque, d'habitude c'est M donc disons M', Ok ?


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2009, 16:53
par Ben314 » 19 Déc 2009, 16:53
Dinozzo13 a écrit:oups, je voulais en fait parler d'un point quelconque, d'habitude c'est M donc disons M', Ok ?
...=3\vec{GM'}
Ca change pas bien le problème : tu as à droite du = tu as un vecteur qui dépend du point quelconque M' alors qu'à gauche du = cela ne dépend pas de M'... c'est plus que louche...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Déc 2009, 22:46
par Dinozzo13 » 19 Déc 2009, 22:46
Alors G est le barycentre de (I,1) et (O,2) donc :

c'est ça que tu me demandes ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2009, 23:06
par Ben314 » 19 Déc 2009, 23:06
Il me semble que, par définition, si G est le barycentre de (I,1) et (O,2) alors :

et cela tombe bien puisque c'est ça qu'on voulait...
Effectivement, cette relation implique que

et cela peut être utile pour la suite...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Déc 2009, 23:11
par Dinozzo13 » 19 Déc 2009, 23:11
Ah je pensais pas du tout à la définition c'était trop simple ça :ptdr: ,
donc on a
= - GM^2+AG^2 - 2 OG^2)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 00:58
par Dinozzo13 » 20 Déc 2009, 00:58
Et que dois-je après avoir obtenu -GM²+IG²-2OG²=0 ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Déc 2009, 01:03
par Ben314 » 20 Déc 2009, 01:03
Vu que tu cherche M, tu fait passer à droite tout ce qui ne contient pas de M, puis tu prend la racine carré des deux cotés et tu tombe sur la définition d'un...
Rappel : A,G et O sont des points parfaitement connus, ce que l'on cherche c'est les points M qui vérifient cette équation...
A la limite, vu que G est le barycentre de (I,1) et (O,2) tu peut aussi écrire AG et OG en fonction de I,O et A...
P.S. je sais pas d'où sort ton point A (faute de frappe ?) il me semble qu'au départ, tu n'avais introduit que O et I (puis G barycentre de O et I)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 01:08
par Dinozzo13 » 20 Déc 2009, 01:08
Eh bien dans ce cas :

,

c'est ça ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Déc 2009, 01:10
par Ben314 » 20 Déc 2009, 01:10
Il me semble qu'on a dit plus haut que, pour que l'expression se simplifie, on devair prendre comme point G le barycentre de (I,1) et (O,2)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 01:11
par Dinozzo13 » 20 Déc 2009, 01:11
Ben314 a écrit:P.S. je sais pas d'où sort ton point A (faute de frappe ?) il me semble qu'au départ, tu n'avais introduit que O et I (puis G barycentre de O et I)
Oui oui, en le refaisant au brouillon j'ai pris A mais il s'agit de I

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Déc 2009, 01:11
par Ben314 » 20 Déc 2009, 01:11
Oui, c'est ça.
Est quel est l'ensemble des point M vérifiant une telle relation ?
(et tu peut toujours exprimer OG et IG en fonction de OI en réutilisant le fait que c'est le barycentre...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 01:14
par Dinozzo13 » 20 Déc 2009, 01:14
C'est un cercle de centre G et de rayon la "racine de ..."

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Déc 2009, 01:19
par Ben314 » 20 Déc 2009, 01:19
C'est exactement ça.
En utilisant la formule que tu as trouvé dans le post #24 et une autre que tu trouvera de la même façon, tu peut aussi simplifier ce qu'il y a sous la racine (tu aurrais même du le faire avant de prendre la racine pour vérifier que tu n'écrit pas la racine d'un nombre... négatif)
Quand tu aura ta solution "géométrique" (en traçant le cercle et la droite du début), tu pourra faire la méthode "algébrique" en remplaçant z par x+iy et en résolvant les systèmes d'équation (tu doit évidement trouver la même chose !!!)....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 01:20
par Dinozzo13 » 20 Déc 2009, 01:20
Je trouve :

et

, mais pourquoi exprimer ces deux vecteurs avec en fonction de
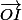
?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 01:31
par Dinozzo13 » 20 Déc 2009, 01:31
Après tout ça je trouve

donc il s'agit d'un cercle de centre

et de rayon

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 01:41
par Dinozzo13 » 20 Déc 2009, 01:41
Etes-vous d'accord ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 14:00
par Dinozzo13 » 20 Déc 2009, 14:00
Etes-vous d'accord ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Déc 2009, 20:19
par Dinozzo13 » 20 Déc 2009, 20:19
Si c'est ça, comment faire pour exprimer les solutions de l'intersection de ce cercle avec la droite précédement trouvée ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Déc 2009, 23:21
par Ben314 » 20 Déc 2009, 23:21
A ta place, arrivé là, je commencerait par faire un joli dessin 'pour voir' (rappel OI=1)
Si tu veut te lancer dans les calculs en partant d'ici, tu dit que le point M a pour coordonnées (x,y), tu traduit en x,y qu'il doit appartenir à la droite, puis idem pour le fait qu'il est sur un cercle et tu cherche à résoudre le système formé des deux équations.
Tu peut aussi tout reprendre du début et écrire z=x+iy et évaluer les trois modules qui doivent être égaux : c'est à peine plus long et on tombe trés vite sur les mêmes deux équations.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
non ?