Bonjour, aujourd'hui, je n'arrive pas à aboutir question ensemble de points, j'aurai donc besoin d'aide, merci encore d'avance ^^.
On me demande de trouver l'ensemble des points

d'affixe

tels que :

Voici comment j'ai procédé :
Pour tout z complexe :

équivaut à

Je m'occupe d'abord de la première équation :

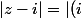(z-1)|)


Soit

et
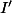
les points de coordonnées respectives
)
et
)
on a donc :

équivaut à

donc :
l'ensemble

des points

du plan complexes est la médiatrice du segment
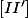
.
Pour la deuxième :

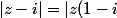|)


Et donc

d'où

et la, je ne sais pas comment déterminer cet ensemble.
Je pense qu'il s'agit d'une droite perpendiculaire à
)
c'est-à-dire l'axe des ordonnées passant par le point

tel que

ai-je bon jusque là ?
