Encore un petit problème avec une équation ...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 13 Sep 2006, 17:17
par Baba » 13 Sep 2006, 17:17
Salut a tous !!
J'ai encore un petit problème ....
Voilà mon énoncé:
Démontrer que l'équation X²-4X+125=0 équivaut à (X-2)²=-121 (c'est fait)
En utilisant i, vérifier que l'équation (X-2)²=-121 a deux solutions 2+11i et 2-11i (ca c'est fait !).
Vérifier, en utilisant les règles de calcul en vigueur dans R et en remplacant i² par -1, que (2-i)^3=2+11i et (2-i)^3=2-11i. (c'est fait aussi !)
Le véritable problème c'est maintenant ....
En déduire des valeurs de u et v, puis l'une des solutions de l'équation x^3=15x+4.
(Sachant que auparavant j'ai deja démontré que u^3 et v^3 étaient solution de la toute prémière équation, et que u^3+v^3=4 et uv=5.
Il faut peut être également savoir que u+v est solution de x^3=15x+4)
Merci d'avance
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 13 Sep 2006, 19:22
par Baba » 13 Sep 2006, 19:22
Personne ne réponds ?
J'ai pas écrit tout ce qu'il fallait ?
-
Jacques COLLOT
- Membre Naturel
- Messages: 76
- Enregistré le: 07 Aoû 2006, 20:07
-
 par Jacques COLLOT » 13 Sep 2006, 20:09
par Jacques COLLOT » 13 Sep 2006, 20:09
Ben, je pense que tu es tout près de la solution.
Si u.v = 5 alors u^3.v^3 = 5^3
tu connais donc la somme et le produit
Alors, u^3 et v^3 sont solutions de l'équation :
X^2-4X+5^3=0
qui comme par hazard a pour solutions :
u^3=2-11i et v^3=2+11i
Tu peux terminer.
Salutations
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 13 Sep 2006, 20:28
par nada-top » 13 Sep 2006, 20:28
Baba a écrit:Il faut peut être également savoir que u+v est solution de x^3=15x+4)
oui c'est juste ::+:: ...aprés avoir trouvé u et v (comme te l'a montré Jacques Collot) tu en déduis u+v et tu vérifie que c une solution.
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 13 Sep 2006, 20:59
par Baba » 13 Sep 2006, 20:59
Excuse moi, mais j'ai pas vraiment compris ce que m'a dit de faire Jaques COLLOT ...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 13 Sep 2006, 21:06
par nada-top » 13 Sep 2006, 21:06
tu dis que t'as démontré que
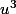
et
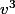
sont solutions de l'équation
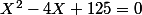
.
et tu as aussi démontré que cette équation a 2 solutions
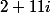
et
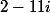
.
donc maintenant tu connais
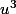
et
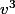
,il ne reste que en déduire

et

.
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 13 Sep 2006, 21:12
par Baba » 13 Sep 2006, 21:12
Ca voudrait dire que u^3=2-11i et v^3=2+11i.
Et donc, on m'aurait fait prouver que (2+i)^3=2+11i et (2-i)^3=2-11i pour avoir les valeurs de u et v implicitement.
C'est bien cela ?
Si c'est bien ca u=2-i et v=2+i.
Non ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 13 Sep 2006, 21:15
par nada-top » 13 Sep 2006, 21:15
oui c bon :happy3:
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 13 Sep 2006, 21:17
par Baba » 13 Sep 2006, 21:17
Ok merci en fait c'était tout bête !!
Comme d'habitude, un grand merci :++:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 13 Sep 2006, 21:18
par nada-top » 13 Sep 2006, 21:18
de rien :happy3:
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 13 Sep 2006, 21:24
par Baba » 13 Sep 2006, 21:24
De rien a toi lol !
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 14 Sep 2006, 21:04
par Baba » 14 Sep 2006, 21:04
Je fais remonter ce post, car par la suite, on me demande d'utiliser les méthodes habituelles pour terminer la résolution de l'équation (x^3= 15x+4).
Le seul truc, c'est que j'y arrive pas ...
Que devrais-je faire ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 14 Sep 2006, 22:40
par nada-top » 14 Sep 2006, 22:40
Salut
il faut résoudre
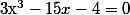
t'as montré que u+v=4 est une solution donc ça revient à résoudre
(x^2+bx+c) = 0)
maintenant il suffit de déterminer b et c (voir
ici) et résoudre une équation de 2ème degré.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
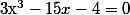
(x^2+bx+c) = 0)
