Encore des divisions euclidiennes

[alexjo59]

[FONT=Comic Sans MS]J'ai encore un petit exercice de divisibilité à faire et apparament, je suis vraiment pas douée dans ce domaine!!!
Pourriez vous me filer un coup de main ou juste me donner quelques pistes svp???
Merci d'avance

1) trouver suivant les valeurs de l'entier naturel n, le reste de la division euclidienne de 3^n par 11
2) en déduire, suivant la valeur du naturel m, les restes de la division euclidienne par 11 des nombres :
A = 1978^m
B = 421^5m + 421^4m + 421^3m + 421^2m + 421^m
on distinguera cinq cas selon la valeur du reste de la division euclidienne de m par 5[/FONT]

[becirj]

1. Il n'y a que 11 restes possibles. Il faut faire les calculs pour n =0 , 1 ...jusqu'à ce que l'on retrouve un reste déjà obtenu puis on peut généraliser en utilisant les congruences.

[allomomo]

Salut,


==>
==>
==>
==>
==>
---------------------------------------

[alexjo59]

[FONT=Comic Sans MS]pourquoi avoir fait 2 parties distingues?[/FONT]

[allomomo]

Re-


C'est periodique !

1,3,9,5,4 puis 1,3,9,5,4 puis 1,3,9,5,4 ....

[alexjo59]

[FONT=Comic Sans MS]a oui d'accord!
j'ai du mal ce soir pour la question 2 je dois utiliser la 1?[/FONT]

[becirj]

Oui, il faut utiliser la première question.
Modulo 11 ,

[alexjo59]

[FONT=Comic Sans MS]oui mais ces nombres sont à la puissance m donc la congruence n'est pas forcément la même pour tous[/FONT]

[becirj]

5 cas possibles d'après la première question :
- Si 2m=5k c'est-à-dire si 2m multiple de 5 ou encore ,
- Si 2m=5k+1 soit ,
...

[alexjo59]

[FONT=Comic Sans MS]à d'accord, je pense avoir compris le truc :id:
et pour le B je procéde donc pareil en additionnant ok
:ptdr: merci beaucoup!!! :++: [/FONT]

[becirj]

On peut ajouter que lorsque
lorsque (car
)
...

[alexjo59]

[FONT=Comic Sans MS] :doh: pouquoi peux-t-on en déduire ça?
je ne comprend pas :mur: [/FONT]

[becirj]

Je le montre d'une autre manière.
On peut établir les relations suivantes modulo 5 :






On voit donc que

[alexjo59]

[FONT=Comic Sans MS]oui je suis d'accord mais ça me sert à quoi dans ma question? :hum: [/FONT]

[becirj]

Parce que dans la question, on précise de distinguer 5 cas suivant les restes dans la division euclidienne de m par 5 (et non de 2m)

[alexjo59]

[FONT=Comic Sans MS]donc je fais , par exemple m congru à 0 modulo 5 puis je calcule la congruence avec 2m, 3m, 4m et 5m et puis j'additionne ce que je trouve et je fais la même chose pour les 4 autres cas?[/FONT]

[becirj]

Pour le deuxième calcul avec 421, modulo 11 donc la somme à calculer
On peut remarquer qu'il s'agit de la somme de 5 termes d'une suite géométrique de premier terme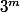 et de raison .

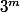Premier cas :si , chaque terme de la somme donc la somme . En d'autres termes, si m est un multiple de 5 alors le reste de la division de la somme par 11 est égal à 5.

Deuxième cas : m ne congrue pas à 0 modulo 5, on utilise la formule pour calculer la somme des termes de la suite géométrique/

mais donc la somme congrue à 0 modulo 11.
On a ainsi montré que si m n'est pas multiple de 5 alors dans la division de la somme par 11, le reste est nul.

[alexjo59]

[FONT=Comic Sans MS] :id: merci beaucoup pour votre aide si précieuse :++: [/FONT]