[SECONDE] Encadrement de la fonction f(x) = (2x-3)/(2-5x)

[paquito]

L'encadrement que tu as trouvé est correct, mais ce n'est pas le meilleur possible puisque tu encadres -2x+3 et que ça permute 7 et 9, ce qui fait apparaître -9/12 et -7/17. Comme te l'as dit chan, la meilleure solution consiste à utiliser le sens de variation de f; ici f est strictement décroissante; donc si tu as a<x<b<2/5 tu as directement f(b)<f(x)<f(a); même chose si tu as 5/2<a<x<b tu as aussitôt f(b)<f(x)<f(a). Essayons de généraliser,donc soit

[paquito]

J'ai fait une fausse manoeuvre; il faut que je réécrive tout! Je le ferait un peu plus tard.

[laetidom]

J'ai fait une fausse manoeuvre; il faut que je réécrive tout! Je le ferait un peu plus tard.

-----------------------------------
merci Paquito pour tout ton travail ainsi qu'à Chan (j'oublie pas Thomas Joseph biensûr), montre moi la suite quand tu peux, il n'y a rien qui presse !, j'imagine que ça doit conduire à l'obtention des -7/12 et -9/17 de Chan...
Bonne soirée de maths à tous ! bye

[paquito]

Salut Laetidum,

En fait, la méthode proposée par chan est un cas particulier d'un résultat très important puisqu'il fait intervenir le sens de variation d'une fonction.
Donc, soit f définie sur I et a et b dans I, si tu sais que f est croissante sur I, a0, elle est croissante et si D0 donc f croît;

si tu pars de -5<x<-1, tu as immédiatement 16/17<f(x)<4;
si tu pars de 0<x<4, tu as immédiatement -1/3<f(x)<11/17;
si tu part de -1<x<0, tu sors du cadre de notre application et tu doit décomposer en -1<x<-3/4 ou -3/4<x<0 qui donne 4<x ou x<-1/3 et donc: x n'appartient pas à ]-1/3; 4[ .

Soit , x0=3/4 et D=-5<0 donc f décroît;

si tu pars de -5<x<-1, tu as immédiatement 4/7<f(x)<16/23;
si tu pars de 1<x<50, tu as immédiatement 149/197<f(x)<2;

Voilà; le plus important finalement, c'est la notion de sens de variations d'une fonction.

[laetidom]

Merci paquito,
Depuis mon lieu de villégiature et avec une tablette, pas facile, je te remercie pour cette explication, à mon retour je la regarderais de près, merci encore, et bonne soirée à tous les matheux...bye

[laetidom]

Bonjour Paquito, bonjour à tous,

Encore merci pour m'avoir bien expliqué la variation, c'est très clair ! (pour info : je sais dériver, faire l'étude de fonction complète)
------------------------
tu m'a écris :

si tu pars de 0<x<4, tu as immédiatement -1/3<f(x)<11/17;
si tu part de -1<x<0, tu sors du cadre de notre application et tu doit décomposer en -1<x<-3/4 ou -3/4<x<0 qui donne 4<x ou x<-1/3 et donc: x n'appartient pas à ]-1/3; 4[ .

je pense que tu voulais écrire plutôt ça

si tu pars de 0<x<4, tu as immédiatement -1/3<f(x)<11/19;
si tu part de -1<x<0, tu sors du cadre de notre application et tu doit décomposer en -1<x<-3/4 ou -3/4<x<0 qui donne 4<f(x) ou f(x)<-1/3 et donc: f(x) n'appartient pas à ]-1/3; 4[ .
------------------------------------------------------------------
Question subsidiaire : je me demandais pourquoi (expliciter la raison svp) le calcul que l'on fait en seconde est moins précis que le résultat que l'on obtient par la variation ? (j'ai bien compris qu'il n'y avait pas de contradiction et que c'étaient 2 mêmes résultats à précision différentes) A quoi cela est dû ? Où dans le calcul perd-on de la précision ? je n'arrive pas à le comprendre......si quelqu'un peut m'expliquer, ça serait sympa !

calcul seconde : f(x)=
2<x<3
1<2x-3<3
8<5x-2<13
<<

<<

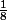
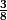
<f(x)<

-0.375<f(x)<-0.0769

encadrement par la variation :

f(x)=

2<x<3

f décroissante sur [2;3]

donc f(3)<f(x)<f(2)

f(3) = (2.3-3)/(2-5.3)=(6-3)/(2-15)=-3/13

f(2)=(2.2-3)/(2-5.2)=(4-3)/(2-10)=-1/8

<f(x)<

-0.231<f(x)<-0.125
-----------------
Merci d'avance

[paquito]

C'est dû au fait que tu encadres le numérateur; donc si -3

[laetidom]

Merci paquito, j'ai compris !!! à la prochaine....merci à tous