Encadrement fonction 1ere S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 12:35
par MissLady » 04 Jan 2015, 12:35
hello,
j'y suis dessus depuis pas mal de temps mais je ne trouve toujours pas la réponse
On prend une fonction f definie sur R tel que f(x) = (7x²+2x-9)
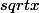
merci d'avance ^^
bonne journée !
-
tototo
- Membre Rationnel
- Messages: 954
- Enregistré le: 08 Nov 2011, 07:41
-
 par tototo » 04 Jan 2015, 13:11
par tototo » 04 Jan 2015, 13:11
MissLady a écrit:hello,
j'y suis dessus depuis pas mal de temps mais je ne trouve toujours pas la réponse
On prend une fonction f definie sur R tel que f(x) = (7x²+2x-9)

merci d'avance ^^
bonne journée !
Bonjour
Lim (x->+infini)f (x)=+infini car c'est les x de plus haut degres qui donne la limite soit x^(3/2).

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Jan 2015, 13:37
par zygomatique » 04 Jan 2015, 13:37
salut
et quelle est la question ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 13:55
par MissLady » 04 Jan 2015, 13:55
oups, je suis désolé, la question est donner un encadrement de f(x) pour x appartient [0;2]
voilà et merci ^^
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 17:14
par MissLady » 04 Jan 2015, 17:14
up merci ^^

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Jan 2015, 18:13
par zygomatique » 04 Jan 2015, 18:13
MissLady a écrit:oups, je suis désolé, la question est donner un encadrement de f(x) pour x appartient [0;2]
voilà et merci ^^
est-il possible de prendre x = 0 ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 18:16
par MissLady » 04 Jan 2015, 18:16
Je ne sais pas, l'énoncer demande de déterminer un encadrement de f(x) pour x appartient à [0;2] c'est tout.
j'ai calculer le delta du trinôme a l'interieur des parenthèse et comme x1 est négatif et x2 positif, je remplace le x par x2. Ai-je juste ??

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Jan 2015, 18:17
par zygomatique » 04 Jan 2015, 18:17
MissLady a écrit:Je ne sais pas, l'énoncer demande de déterminer un encadrement de f(x) pour x appartient à [0;2] c'est tout.
j'ai calculer le delta du trinôme a l'interieur des parenthèse et comme x1 est négatif et x2 positif, je remplace le x par x2. Ai-je juste ??
n'importe quoi ...
mais bon si tu ne sais pas répondre à ma question ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 18:20
par MissLady » 04 Jan 2015, 18:20
??? n'importe quoi ? pour ta question oui il est possible de prendre x= 0 car l'encadrement est fermé donc la valeur 0 est accepté
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 18:48
par MissLady » 04 Jan 2015, 18:48
up s'il vous plait

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Jan 2015, 19:17
par zygomatique » 04 Jan 2015, 19:17
MissLady a écrit:??? n'importe quoi ? pour ta question oui il est possible de prendre x= 0 car l'encadrement est fermé donc la valeur 0 est accepté
ha bon ? ...

f(x) = .... ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 19:24
par MissLady » 04 Jan 2015, 19:24
f(0) = (7*0^2+ 2*0-9)

= 0

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Jan 2015, 19:32
par zygomatique » 04 Jan 2015, 19:32
MissLady a écrit:f(0) = (7*0^2+ 2*0-9)

= 0
un peu de sérieux !!!
regarde ton énoncé ::
On prend une fonction f definie sur R tel que f(x) = (7x²+2x-9)/
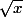
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 04 Jan 2015, 19:37
par MissLady » 04 Jan 2015, 19:37
zygomatique a écrit:un peu de sérieux !!!
regarde ton énoncé ::
Désolée, c'est la fatigue ^^'
c'est impossible ?! car après rectification, on a -9/

je me trompe peut être, sûr je dirais même
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 10 Jan 2015, 11:35
par MissLady » 10 Jan 2015, 11:35
Up merci, je n'ai toujours pas retrouvé la réponse....
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 10 Jan 2015, 12:44
par nodjim » 10 Jan 2015, 12:44
Il faut exclure 0 de l'intervalle. Sinon, pour l'encadrement, il faut connaitre les valeurs extrêmes, et donc pour ça étudier la variation de la fonction, et donc l'étude de la dérivée est un bon moyen.
-
maths-lycee fr
- Membre Relatif
- Messages: 206
- Enregistré le: 16 Juil 2014, 23:15
-
 par maths-lycee fr » 10 Jan 2015, 13:04
par maths-lycee fr » 10 Jan 2015, 13:04
tototo a écrit:Bonjour
Lim (x->+infini)f (x)=+infini car c'est les x de plus haut degres qui donne la limite soit x^(3/2).
Bonjour,
Pour info, les limites ne sont plus au programme de première S depuis quelques années déjà et non plus au programme de terminale ES...
J-F L
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 10 Jan 2015, 13:20
par MissLady » 10 Jan 2015, 13:20
je suis perdue, je ne comprend tes explications nodjim :/
En première S on fait les limite quand h tend vers 0, c'est tout ^^'
merci beaucoup de vos réponses
-
MissLady
- Membre Naturel
- Messages: 76
- Enregistré le: 01 Oct 2014, 14:23
-
 par MissLady » 10 Jan 2015, 15:00
par MissLady » 10 Jan 2015, 15:00
je viens de rectifier l'énoncé, car ce n'est pas le tout divisé par
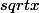
, mais multiplié ^^' veuillez m'excuser pour cette grossière erreur....

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 10 Jan 2015, 15:14
par capitaine nuggets » 10 Jan 2015, 15:14
Salut !
En justifiant, si x\in [0,2] alors on a \sqrt x \in [0,2].
Mais le problème est qu'à priori, on n'a pas

implique

.
Je te propose donc d'écrire

sous forme canonique, en montrant que :
[CENTER]
^2 + k \right])
[/CENTER]
où

est une certaine constante que tu préciseras :+++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités