Salut,
Il manque une parenthèse dans ton expression :

=
^{n} +20)
Si tu laisses sans parenthèse, la puissance ne s'appliquera qu'au numérateur (donc 1^n) et ta suite sera alors constante.
Pour passer de l'étape 1 à l'étape 2, il faudrait théoriquement justifier que

est croissante sur

, ce qui justifiera que tu ne changes pas le sens de l'inégalité é l'étape 2.
C'est bien sûr vrai puisque
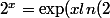))
.
Mais bon franchement, y'a vraiment pas besoin de présenter les choses mécaniquement comme tu le fais.
Tu peux dire que

(le double d'un nombre
positif est plus grand que ce nombre) donc

Puis poursuivre.
Et à la limite, tu peux même directement dire que :
^{n} \times \frac{1}{2} \leq (\frac{1}{2})^{n})
(la moitié d'un nombre positif est plus petite que le nombre)
Pseudo modifié : anciennement Trident2.
