Bonsoir,
Veuillez m'aider s'il vous plaît
Dans le plan complexe muni d'un repère orthonormal direct (o;u(vecteur);v(vecteur)) on considère le point A d'affixe a=1+iV3 et le point B d'affixe b=1-iV3 et le point C' milieu de [AB]
1) a) Déterminer l'affixe c' de C' et Déterminer l'affixe c de C image de A par la rotation de centre O et pi /2
2) a) Déterminer l'affixe m de M image de C' par l'homothétie de centre C et de rapport 2/3.
Que peut-on dire du point M pour le triangle ABC?
3) a)Déterminer l'affixe n de N image d C par la translation du vecteur 2u
et calculer (c-d)/(n-a). que peut-on déduire?
1/a/ 2/a/3/a/je bloque
Merci beaucoup:we: :hein: :doh:
écriture complexe des transformations usuelles
7 messages
- Page 1 sur 1
Bonjour
Si zA est l'affixe de A et zB l'affixe de B , l'affixe du milieu est :
1/2 (zA + zB) (était il nécessaire de le dire ?)
Tout l'exo est l'application de formules qui figurent dans le cours
Une vérification géométrique est possible ( les rotations, translations etc sont vues en seconde et avant )
Si zA est l'affixe de A et zB l'affixe de B , l'affixe du milieu est :
1/2 (zA + zB) (était il nécessaire de le dire ?)
Tout l'exo est l'application de formules qui figurent dans le cours
Une vérification géométrique est possible ( les rotations, translations etc sont vues en seconde et avant )
1/C' est milieu de [AB] alors  c'est pourtant du cours !!
c'est pourtant du cours !!
2/Déterminer l'affixe m de M image de C' par l'homothétie de centre C et de rapport 2/3. => donc H(C,2/3) teq que H(C')=M
Mtn t'es cap pour résoudre 3/
PS : Si K et L deux points du plan dont leurs sont affixes sont succéssivement k et l alors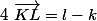
2/Déterminer l'affixe m de M image de C' par l'homothétie de centre C et de rapport 2/3. => donc H(C,2/3) teq que H(C')=M
Mtn t'es cap pour résoudre 3/
PS : Si K et L deux points du plan dont leurs sont affixes sont succéssivement k et l alors
Les multiples ne doivent pas être utilisés sans nécessité
écriture complexe des transformations usuelles
Bonjour,
Je vais t'aider pour le
1)a)
c' = 1
c = i
Merci beaucoup :we: :doh:
Je vais t'aider pour le
1)a)
c' = 1
c = i
Merci beaucoup :we: :doh:
Toshiba a écrit:Bonjour,
Je vais t'aider pour le
1)a)
c' = 1
c = i
Merci beaucoup :we: :doh:
Tu vas m'aider ??!!!
Non merci j'ai pas besoin d'aide !!!
Ah ok !! ben non je te donnerai pas des réponses tu dois les trouver tout seul !! Je t'ai déja tout les formules dont tu as besoin !!!
A toi de jouer !!
Les multiples ne doivent pas être utilisés sans nécessité
écriture complexe d'une homothétie
Bonjour,
j'ai besoin de votre aide de toute urgence s'il vous plait!
Dans le plan complexe muni d'un repère orthonormal direct (O;U(vecteur),V(Vecteur)) (unité graphique:3 cm),on considère le point A d'affixe 2i et le point B d'affixe 1.
1/Déterminer et construire l'ensemble E des points M d'affixe z tels que : lz-2il=V5.
1/. Ensemble E
------------------
Ton équation est équivalente à chercher les points M tels que
AM = ;)5
C'est donc un cercle de centre A de rayon ;)5.
Il reste donc à le déterminer par le calcul.
2/Déterminer et construire l'ensemble F des points M d'affixe z tels que :lz-2il/lz-1l=1
2/. Ensemble F
------------------
Ici l'équation est équivalente à AM = MB (avec z ;) 1)
Donc ceci correspond à la médiatrice de [AB].
On doit obtenir une équation de droite.
3/Déterminer et construire l'image E' de E par l'homothétie de centre O et de rapport 1/2.
3/. Ensemble E'
------------------
L'homothétique d'un cercle est un cercle dont le centre A' est l'image de A et le rayon est kR où k est le rapport d'homothétie.
4/Déterminer et construire l'image F' de F par la rotation de centre O et d'angle pi/2.
4/. Ensemble F'
-------------------
L'image d'une droite par une rotation est aussi une droite.
Il reste donc à traduire en complexes.
Merci beaucoup :we: :doh:
j'ai besoin de votre aide de toute urgence s'il vous plait!
Dans le plan complexe muni d'un repère orthonormal direct (O;U(vecteur),V(Vecteur)) (unité graphique:3 cm),on considère le point A d'affixe 2i et le point B d'affixe 1.
1/Déterminer et construire l'ensemble E des points M d'affixe z tels que : lz-2il=V5.
1/. Ensemble E
------------------
Ton équation est équivalente à chercher les points M tels que
AM = ;)5
C'est donc un cercle de centre A de rayon ;)5.
Il reste donc à le déterminer par le calcul.
2/Déterminer et construire l'ensemble F des points M d'affixe z tels que :lz-2il/lz-1l=1
2/. Ensemble F
------------------
Ici l'équation est équivalente à AM = MB (avec z ;) 1)
Donc ceci correspond à la médiatrice de [AB].
On doit obtenir une équation de droite.
3/Déterminer et construire l'image E' de E par l'homothétie de centre O et de rapport 1/2.
3/. Ensemble E'
------------------
L'homothétique d'un cercle est un cercle dont le centre A' est l'image de A et le rayon est kR où k est le rapport d'homothétie.
4/Déterminer et construire l'image F' de F par la rotation de centre O et d'angle pi/2.
4/. Ensemble F'
-------------------
L'image d'une droite par une rotation est aussi une droite.
Il reste donc à traduire en complexes.
Merci beaucoup :we: :doh:
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
