Bonjour à tous,j'ai quatre exercices de math à faire pour lundi et j'ai réussi les deux premiers mais celui-la je n'y arrive pas.Merci d'avance pour votre aide.
Préciser les positions relatives des droites d et d de lespace.
La droite d est engendrée par le point A ( 1 ; -1 ; 1) et le vecteur u (1 ; 2 ; -3)
La droite d est engendrée par le point B ( 2 ; 2 ; 3) et le vecteur v ( 1 ; 1 ; 1)
PS:je ne sais meme pas la signification du mot " engendrée"
Droite de l'espace
3 messages
- Page 1 sur 1
Bonjour
D'abord, les positions relatives de 2 droites de l'espace sont
coplanaires : dans ce cas, elles sont parallèles , confondus ou ont un point commun (coplanaire = elles appartiennent à un même plan)
non coplanaire : dans ce cas, elles ont aucun point commun ou elles sont orthogonales.
Le mot engendré signifie que le vecteur est un vecteur directeur de d
est un vecteur directeur de d
Calculons les équations des droites d : engendrée par le passons par le point
passons par le point )
La méthode ci-dessus est une méthode générale pour la recherche d'une équation de droite (dans l'espace et le plan)
1)Soit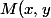) un point de la droite
un point de la droite
2)Comme est un vecteur directeur de d, les vecteurs
est un vecteur directeur de d, les vecteurs 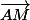 et
et  sont colinéaires
sont colinéaires
Par définition, il existe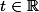 tel que
tel que 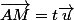
3)Tu écris le système avec les équations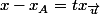 et
et 
4)Tu écris en fonction de
en fonction de  . On note ces expressions C et D
. On note ces expressions C et D
5) Tu écris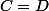 , par transformation d'écriture tu obtiens ton équation de la droite d.
, par transformation d'écriture tu obtiens ton équation de la droite d.
Pour connaître maintenant la position relative des 2 droites ,
a) Tu vérifies si ces 2 vecteurs et
et  sont colinéaires (2 vecteurs sont colinéaires si les coordonnées de l'un sont proportionnelles aux coordonnées de l'autre) alors tes droites sont soient parallèles soient confondues : dans ce cas, les droites d et d' sont coplanaires.
sont colinéaires (2 vecteurs sont colinéaires si les coordonnées de l'un sont proportionnelles aux coordonnées de l'autre) alors tes droites sont soient parallèles soient confondues : dans ce cas, les droites d et d' sont coplanaires.
b) Cherche les points communs des deux droites .
Si tu trouves un point en commun alors elles sont sécantes (donc coplanaires) (en particulier regardes si les vecteurs et
et  sont orthogonaux : calcule le produit scalaire
sont orthogonaux : calcule le produit scalaire 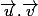 si le résultat est nul alors ces vecteurs sont orthogonaux) .
si le résultat est nul alors ces vecteurs sont orthogonaux) .
S'il s'agit de la même équation de droite (l'une des équations de droites est celle l'autre que l'on a multiplié par un réel) alors tes droites sont confondues.
c)S'il n'y a pas de point commun alors tes droites ne sont pas coplanaires
D'abord, les positions relatives de 2 droites de l'espace sont
coplanaires : dans ce cas, elles sont parallèles , confondus ou ont un point commun (coplanaire = elles appartiennent à un même plan)
non coplanaire : dans ce cas, elles ont aucun point commun ou elles sont orthogonales.
Le mot engendré signifie que le vecteur
Calculons les équations des droites d : engendrée par le
La méthode ci-dessus est une méthode générale pour la recherche d'une équation de droite (dans l'espace et le plan)
1)Soit
2)Comme
Par définition, il existe
3)Tu écris le système avec les équations
4)Tu écris
5) Tu écris
Pour connaître maintenant la position relative des 2 droites ,
a) Tu vérifies si ces 2 vecteurs
b) Cherche les points communs des deux droites .
Si tu trouves un point en commun alors elles sont sécantes (donc coplanaires) (en particulier regardes si les vecteurs
S'il s'agit de la même équation de droite (l'une des équations de droites est celle l'autre que l'on a multiplié par un réel) alors tes droites sont confondues.
c)S'il n'y a pas de point commun alors tes droites ne sont pas coplanaires
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
