Domaine de définition des fonctions rationnelle.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 15 Juin 2015, 16:10
Bonjour
Pour le moment, je n'ai pas encore de travaillé avec les fonction rationnelle (avec racine carré).
Voici des exercices sur le domaine de définition des fonctions rationnelle.
 = sqrt{x^2-x-2})
Je pense qu'il faut résoudre cette équation du second degré.
^2 -4*1*(-2) = 1-4* (-2) = 1-(-8)=9)
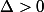
on cherche
et
 + sqrt{9}}{2} = \frac{1 + 3}{2} = \frac{4}{2} = 2)
 - sqrt{9}}{2} = \frac{1 - 3}{2} = \frac{-2}{2} = -1)
Donc
.
Pour
 = sqrt{-x^2+x-2})
*(-2) = 1-8 = -7)
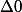
-4*1*6 = 25-24 = 1)
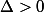
, on cherche
et
.
 + sqrt{1}}{2} = \frac{-(-5) + 1}{2} = \frac{5 + 1}{2} = \frac{6}{2} = 3)
 - sqrt{1}}{2} = \frac{-(-5) - 1}{2} = \frac{5 - 1}{2} = \frac{4}{2} = 2)
Donc
Pour
=sqrt{\frac{3x+1}{4x2}})
On doit avoir
soit
On doit avoir
soit
soit
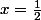
Donc
.
Pour
=sqrt{2x+5}-\frac{1}{x-2})
On a x-2 =0 x=2 soit
Est-ce que c'est correct ?
A +
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Juin 2015, 16:28
salut
ce ne sont pas de fonction rationnelle !!!
et la racine de 0 existe ....
donc mauvaise condition pour f et faux pour h ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 28 Juin 2015, 11:20
Bonjour
Que dois t-on faire quand on a des fonction comme f et H ?
A +
-
mathelot
par mathelot » 28 Juin 2015, 11:31
novicemaths a écrit:Pour
 = \frac{1}{sqrt{x^2-5x+6}})
Donc
ax^2+bx+c est du signe de a à l'extérieur de l'intervalle des racines.
-
Frangine
- Membre Rationnel
- Messages: 933
- Enregistré le: 13 Nov 2005, 08:15
-
par Frangine » 28 Juin 2015, 12:01
Bonjour,
Essayer de voir le programme de 1ère en sortant de seconde part d'un certain sentiment , je ne crois pas que cela soit très bon quand on applique des formules dont on ne comprend pas l'utilité !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
