Bonjour,
voilà j'ai un problème avec la méthode de Hörner lorsque le binôme diviseur est de ce type
(2 x-3)
Donc lorsque le "x" a un coefficient outre que 1.
Sinon, je sais parfaitement utiliser la grille de Hörner, et aussi avoir réussi ce genre de division décrite ci-dessus, mais après un certain temps j'ai oublié, et je n'y arrive plus.
Donc voilà, si vous pourriez m'aider à m'expliquer comment faire, merci (je sais que ça tombe en fraction, mais pour faire la, grille, il faut faire parfois de modifications, je pense, donc...)
Voici un exercice pour m'expliquer:
(15x;)+x³-6x²+21x+18) : (3x+2)
Division euclidienne (Hörner)
14 messages
- Page 1 sur 1
par LeJeu » 29 Aoû 2012, 18:49
Littlemathy a écrit:Bonjour,
voilà j'ai un problème avec la méthode de Hörner lorsque le binôme diviseur est de ce type
(2 x-3)
Donc lorsque le "x" a un coefficient outre que 1.
Sinon, je sais parfaitement utiliser la grille de Hörner, et aussi avoir réussi ce genre de division décrite ci-dessus, mais après un certain temps j'ai oublié, et je n'y arrive plus.
Donc voilà, si vous pourriez m'aider à m'expliquer comment faire, merci (je sais que ça tombe en fraction, mais pour faire la, grille, il faut faire parfois de modifications, je pense, donc...)
Voici un exercice pour m'expliquer:
(15x;)+x³-6x²+21x+18) : (3x+2)
Je te proposerais de contourner Horner ( que je ne connaissais pas avant ce soir) en faisant une division classique
"en 15 x;) combien il y a de 3x : 5 x³"
tu multiplies (3x+2) par 5 x³ et tu soustrais
reste :-9x³-6x²+21x+18
" en -9x³" combien il y a de 3x : -3x²
tu multiplies (3x+2) par -3x² et tu soustrais
reste : 21x+18
Et la ca doit tomber pile ....
ce n'est pas le cas : -2/3 n'est pas une racine évident de ton polynome....
Tu as mal fabriqué ton exemple
si tu prends plutôt (15x;)+x³-6x²+21x+14)
alors tu arrives à 21x +14 = 7 ( 3x+2)
et donc (15x;)+x³-6x²+21x+14) = ( 3x+2) ( 5 x³ -3x² +7)
Ok ?
par Littlemathy » 29 Aoû 2012, 18:54
:help:
Je vois, mais pour mon cours je dois pouvoir appliquer Hörner, et cet exemple est tiré de mon cours
Personne d'autre pour une version avec une grille de Hörner? :help:
LeJeu a écrit:Je te proposerais de contourner Horner ( que je ne connaissais pas avant ce soir) en faisant une division classique
"en 15 x;) combien il y a de 3x : 5 x³"
tu multiplies (3x+2) par 5 x³ et tu soustrais
reste :-9x³-6x²+21x+18
" en -9x³" combien il y a de 3x : -3x²
tu multiplies (3x+2) par -3x² et tu soustrais
reste : 21x+18
Et la ca doit tomber pile ....
ce n'est pas le cas : -2/3 n'est pas une racine évident de ton polynome....
Tu as mal fabriqué ton exemple
si tu prends plutôt (15x;)+x³-6x²+21x+14)
alors tu arrives à 21x +14 = 7 ( 3x+2)
et donc (15x;)+x³-6x²+21x+14) = ( 3x+2) ( 5 x³ -3x² +7)
Ok ?
Je vois, mais pour mon cours je dois pouvoir appliquer Hörner, et cet exemple est tiré de mon cours
Personne d'autre pour une version avec une grille de Hörner? :help:
par LeJeu » 29 Aoû 2012, 18:56
Littlemathy a écrit::help:
Je vois, mais pour mon cours je dois pouvoir appliquer Hörner, et cet exemple est tiré de mon cours
Personne d'autre pour une version avec une grille de Hörner? :help:
Tu m'étonnes.. quelle que soit la méthode il faut quand même que ce soit divisible .....Un erreur de recopie ?
par chan79 » 29 Aoû 2012, 19:01
LeJeu a écrit:Tu m'étonnes.. quelle que soit la méthode il faut quand même que ce soit divisible .....Un erreur de recopie ?
salut
pour la méthode de Hörner, il faut connaître une racine (évidente) je crois
Sinon, si tu poses la division euclienne de ce polynôme par 3x+2, il y a un reste de 4
par beagle » 29 Aoû 2012, 19:02
LeJeu a écrit:Tu m'étonnes.. quelle que soit la méthode il faut quand même que ce soit divisible .....Un erreur de recopie ?
non, faut pas que cela soit divisible, on note du reste comme dans la division euclidienne
et cela marche divisible si on avait 14 au lieu de 18,
donc cela va se factoriser avec un reste de 4,
mais comme j'ai fait avec Yvette Horner, faudra attendre un autre intervenant
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
par LeJeu » 29 Aoû 2012, 19:04
chan79 a écrit:salut
pour la méthode de Hörner, il faut connaître une racine (évidente) je crois
Sinon, si tu poses la division euclienne de ce polynôme par 3x+2, il y a un reste de 4
Littlemathy... on est donc deux à trouver qu'il reste 4 .....
Sinon pour horner : il faut diviser par ( x +2/3) , avec la version corrigée du plynome que je t'ai donné !
[edit] non trois maintenant ! salut beagle !
par beagle » 29 Aoû 2012, 19:07
Content de te revoir LeJeu, t'étais dans ton rally tout ce temps là?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
par LeJeu » 29 Aoû 2012, 19:16
beagle a écrit:Content de te revoir LeJeu, t'étais dans ton rally tout ce temps là?
J'aime bien faire des pauses pour me ressourcer ! sinon effectivement je suis en train de préparer un petit truc sympa pour novembre ( ce que tu appelles un rallye ...)
J'ai pas encore lu les derniers posts : pas de psychodrames ces derniers temps ?
Bon ok !je vais tenter d'assurer une présence un peu moins en pointillé !
Littlemathy a écrit:Je vois, mais pour mon cours je dois pouvoir appliquer Hörner
Tu sais Littlemathy, tu devrais faire confiance et ne pas t'accrocher tant au cours, une division reste une division...... quelle que soit la méthode
par beagle » 29 Aoû 2012, 21:16
Bon, alors avec l'exemple pourri de wiki + du beagle,
+yvette horner
première rangée A les coefs qs
15 1 -6 21 18
la deuxième rangée B sert à compter les -2 ou les plus 2, enfin bref,
faudra multipler la dernière rangée par -2 car c'est pour du x-a et ici x- (-2)
la troisième rangée C sera du x3 des 3x,
elle n'existe peut-ètre pas dans la grille d'horner, mais oui dans la beagle horner
la quatrième rangée D divise par 3 la troisième rangée
donc attention, c'est parti:
15 sur A, 0 sur B
15+0=15 sur C
15/3=5 sur D
ce 5 va fois -2 donner -10 en B sous le 1 de A, cela fera -9 en C (-10+1) divisé par 3 qui donne -3 en D
ce-3 fois -2 va faire du +6 en B, du 0 en C, du 0 en D
ce 0 fera du fois-2 est 0 en B, du 21-0 fait 21 en c, du 21/3 fait 7 en D
ce 7 fera du -2 fois 7 est -14 en B, +4 qui est le reste
soit
A=15.1. .-6. 21. 18
B= 0-10.+6.0. -14
C=15.-9.0..21..+4
D=5.-3..0..7.. reste4
peut-ètre que Horner reste à 3 rangées, on passe directement à D sans rangée C,
mais perso je suis obligé de brancher mon cray à la maison pour diviser par 3 , alors, ...
+yvette horner
première rangée A les coefs qs
15 1 -6 21 18
la deuxième rangée B sert à compter les -2 ou les plus 2, enfin bref,
faudra multipler la dernière rangée par -2 car c'est pour du x-a et ici x- (-2)
la troisième rangée C sera du x3 des 3x,
elle n'existe peut-ètre pas dans la grille d'horner, mais oui dans la beagle horner
la quatrième rangée D divise par 3 la troisième rangée
donc attention, c'est parti:
15 sur A, 0 sur B
15+0=15 sur C
15/3=5 sur D
ce 5 va fois -2 donner -10 en B sous le 1 de A, cela fera -9 en C (-10+1) divisé par 3 qui donne -3 en D
ce-3 fois -2 va faire du +6 en B, du 0 en C, du 0 en D
ce 0 fera du fois-2 est 0 en B, du 21-0 fait 21 en c, du 21/3 fait 7 en D
ce 7 fera du -2 fois 7 est -14 en B, +4 qui est le reste
soit
A=15.1. .-6. 21. 18
B= 0-10.+6.0. -14
C=15.-9.0..21..+4
D=5.-3..0..7.. reste4
peut-ètre que Horner reste à 3 rangées, on passe directement à D sans rangée C,
mais perso je suis obligé de brancher mon cray à la maison pour diviser par 3 , alors, ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
par LeJeu » 29 Aoû 2012, 21:26
beagle a écrit:Bon, alors avec l'exemple pourri de wiki + du beagle,
+yvette horner
J'ai pas tout vérifié ... mais çà ressemble à ce qu'attendait Yvette..
Moi je dis qu'une division à la con de polynome donne la même chose en plus compréhensible
Bravo Beagle pour l'effort !
par C.Ret » 30 Aoû 2012, 08:58
Bonjour,
Pour ma part, j'effectue ce type de division euclidienne de polynôme avec une méthode personnelle. J'apprends en lisant ce fils qu'il s'agit en fait d'une méthode "à la Horner" car le calcul est réalisé dans un tableau.
Je décompose la méthode avec le polynôme donné en exemple:
=15x^4+x^3-6x^2+21x+18)
Nous cherchons les coefficients du polynôme Q et le reste tel que=(3x+2).Q(x)+r)
où )
sera donc un polynôme d'un degré inférieur à )
(soit 3).
Je reporte donc les coefficients de)
dans le tableau:
 &|& 15 & 1 & -6 & 21 &|& 18 \\<br />3x+2&|& & & & & &\\ <br /> Q(x) &|& & & & &<br />\end{matrix})
Puis, j'effectue la "division" selon le principe que je sais maintenant être celui de Horner. Comme il y a un coefficient 3 devant x, il faut donc diviser par celui-ci le coefficient correspondant de P(x)
& | &15&1&-6&21& | 18\\<br />3x+2& | &\frac{15}{3}& & & & \\ <br />Q(x)& | & & & & <br />\end{matrix})
Par chance, dans cet exemple on obtient des fractions entières. Ce qui rend les choses plus lisibles et les calculs plus simples.
On reporte le résultat de la "division" dans la ligne des coefficient de:
& | &15&1&-6&21& | 18\\<br />3x+2& | &\frac{15}{3}& & & & \\ <br />Q(x)& | & 5 & & & <br />\end{matrix})
Pour les coefficients suivants, les choses se compliquent car le "+2" du monôme intervient. Il faut donc ne pas oublier de retirer du coefficient reporté depuis P(x) deux fois la valeur du coefficient précédant de la ligne:
& | &15&1&-6&21& | 18\\<br />3x+2& | &\frac{15}{3}&\frac{1-2\times5}{3}& & & \\ <br />Q(x)& | & 5 & & & <br />\end{matrix})
On simplifie cette fraction et on reporte le coefficient obtenu dans la ligne Q(x). Ici aussi on a la chance d'avoir une valeur entière :
& | &15&1&-6&21& | 18\\<br />3x+2& | &\frac{15}{3}&\frac{1-2\times5}{3}& & & \\ <br />Q(x)& | &5&-3& & <br />\end{matrix})
On continue ainsi de suite jusqu'à la dernière colonne qui concerne alors le reste de la division euclidienne (et qui donc a un trainement un peu diffèrent).
& | &15&1&-6&21& | &18\\<br />3x+2& | &\frac{15}{3}&\frac{1-2\times5}{3} & \frac{(-6)-(-3)\times2}{3}&\frac{21-0\times2}{3}& | & \\ <br />Q(x)& | &5&-3&0&7& | &<br />\end{matrix})
Pour cette dernière colonne, il n'y a plus intervention du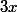
, donc plus de division par trois: On ne s'occupe que des termes sans 
:
& | &15&1&-6&21& | &18\\<br />3x+2& | &\frac{15}{3}&\frac{1-2\times5}{3} & \frac{(-6)-(-3)\times2}{3}&\frac{21-0\times2}{3}& | & 18-7\times2\\ <br />Q(x)& | &5&-3&0&7& | &4<br />\end{matrix})
Un fois le tableau complété, on l'interprète en lisant les coefficients de dans la dernière ligne ainsi que le reste:
=15x^4+x^3-6x^2+21x+18=(3x+2).Q(x)+r=(3x+2).(5x^3-3x^2+7)+4)
soit
=5x^3-3x^2+7)
et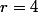 
On constatera que c'est exactement la méthode décrite et décomposée ci-dessus par Beagle !
(C'est l'avantage du VAX par rapport au Cray, on peut lui faire faire plus de chose à chaque étape !).
Pour ma part, j'effectue ce type de division euclidienne de polynôme avec une méthode personnelle. J'apprends en lisant ce fils qu'il s'agit en fait d'une méthode "à la Horner" car le calcul est réalisé dans un tableau.
Je décompose la méthode avec le polynôme donné en exemple:
Nous cherchons les coefficients du polynôme Q et le reste tel que
Je reporte donc les coefficients de
Puis, j'effectue la "division" selon le principe que je sais maintenant être celui de Horner. Comme il y a un coefficient 3 devant x, il faut donc diviser par celui-ci le coefficient correspondant de P(x)
Par chance, dans cet exemple on obtient des fractions entières. Ce qui rend les choses plus lisibles et les calculs plus simples.
On reporte le résultat de la "division" dans la ligne des coefficient de
Pour les coefficients suivants, les choses se compliquent car le "+2" du monôme intervient. Il faut donc ne pas oublier de retirer du coefficient reporté depuis P(x) deux fois la valeur du coefficient précédant de la ligne
On simplifie cette fraction et on reporte le coefficient obtenu dans la ligne Q(x). Ici aussi on a la chance d'avoir une valeur entière :
On continue ainsi de suite jusqu'à la dernière colonne qui concerne alors le reste de la division euclidienne (et qui donc a un trainement un peu diffèrent).
Pour cette dernière colonne, il n'y a plus intervention du
Un fois le tableau complété, on l'interprète en lisant les coefficients de
soit
On constatera que c'est exactement la méthode décrite et décomposée ci-dessus par Beagle !
(C'est l'avantage du VAX par rapport au Cray, on peut lui faire faire plus de chose à chaque étape !).
par beagle » 30 Aoû 2012, 11:02
Voilà qui est très bien expliqué!
Eh oui, tu faisais du Horner sans le savoir!
Eh oui, tu faisais du Horner sans le savoir!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
par Littlemathy » 30 Aoû 2012, 15:52
Waow, merci pour tous vos efforts sur ce calcul!
Beagle, c'est effectivement un peu comme la méthode horner, mais avec une étape en plus! Je vais me pencher dessus!
C.Ret, je pense que je pourrai utiliser cette technique pour ce genre de calcul qui me pose problème :) Ca m'impressionne à chaque fois que vous me répondiez tous avec les bonnes réponses, avec vos techniques alors que moi j'ai déjà du mal à utiliser celle qu'on m'a apprise! ^^
Sinon comme dis Lejeu, je peux faire une bête division euclidienne, sans horner, mais comme ce serait pour un contrôle assez sérieux, le prof pourrait penser que je ne sais pas utiliser la méthode horner, et me retirer des points! :S :doh:
Beagle, c'est effectivement un peu comme la méthode horner, mais avec une étape en plus! Je vais me pencher dessus!
C.Ret, je pense que je pourrai utiliser cette technique pour ce genre de calcul qui me pose problème :) Ca m'impressionne à chaque fois que vous me répondiez tous avec les bonnes réponses, avec vos techniques alors que moi j'ai déjà du mal à utiliser celle qu'on m'a apprise! ^^
Sinon comme dis Lejeu, je peux faire une bête division euclidienne, sans horner, mais comme ce serait pour un contrôle assez sérieux, le prof pourrait penser que je ne sais pas utiliser la méthode horner, et me retirer des points! :S :doh:
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :