2^pq - 1 divisible par ... (spé math, term S)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 19 Nov 2005, 22:19
par skyskiper » 19 Nov 2005, 22:19
Voilà, j'ai une question en spé math qui me taquine un peu les neuronnes et je n'arrive pas à trouver le chemin vers la solution. Si quelqu'un a la gentillesse de m'aider, ce serait super sympa!
Voilà ma question:
"Si p et q sont deux entier naturels non nuls, 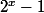 (avec x=p.q) est divisible par
(avec x=p.q) est divisible par 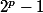 et par
et par 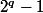 , cette affirmation est-elle vrai ou fausse?"
, cette affirmation est-elle vrai ou fausse?"J'aimerai qu'on me donne une piste et pas une réponse svp, ça me permettrai de trouver seul.
Merci à ceux qui auront le courage de m'aider!
++ :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 19 Nov 2005, 22:25
par Zebulon » 19 Nov 2005, 22:25
Bonsoir,
voici une petite indication:
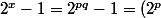}^q-1^q={(2^q)}^p-1^p)
A toi de trouver...
Bon courage et à bientôt,
Zeb.
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 20 Nov 2005, 12:06
par skyskiper » 20 Nov 2005, 12:06
Zebulon a écrit:Bonsoir,
voici une petite indication:
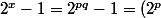}^q-1^q={(2^q)}^p-1^p)
A toi de trouver...
Bon courage et à bientôt,
Zeb.
Salut Zebulon, merci pour ton aide mais je n'avance toujours pas. J'avais déjà pensé à ton indication mais cela ne ma pas permis de trouver de méthode...
Il faut utiliser les congruences? le PGCD? la divisibilité? J'ai essayer pas mal de chemin mais je n'y arrive pas... :triste:
Si tu peux me donner une petite indication en plus, ce serait sympa...
Merci!
++
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 20 Nov 2005, 12:07
par skyskiper » 20 Nov 2005, 12:07
J'ai aussi penser au fait qu'on puisse poser
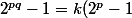=k'(2^q-1))
mais ça ne me donne rien...
++
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 20 Nov 2005, 12:49
par Zebulon » 20 Nov 2005, 12:49
Bonjour,
je te pose un problème qui te permettra d'avancer et de connaître une formule de plus!
Calcule :
[a^{n-1}+a^{n-2}+...+a^2+a+1])
.
Et essaie d'en déduire les divisibilités demandées... :++:
Bon courage!
Zeb.
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 20 Nov 2005, 19:10
par skyskiper » 20 Nov 2005, 19:10
Zebulon a écrit:Bonjour,
je te pose un problème qui te permettra d'avancer et de connaître une formule de plus!
Calcule :
[a^{n-1}+a^{n-2}+...+a^2+a+1])
.
Et essaie d'en déduire les divisibilités demandées... :++:
Bon courage!
Zeb.
Merci pour ton aide, voilà ce que j'ai trouver:
(a^{n-1}+a^{n-2}+...+a^2+a+1) <br />= a^n+a^{n-1}+...+a^3+a^2+a-a^{n-1}-a^{n-2}-...-a^2-a-1<br /> = a^n-1)
Ainsi je peux écrire que
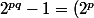^q-1=(2^p-1)(2^{q-1}+2^{q-2}+...+2^2+2+1))
d'où
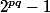
est divisible par
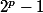
.
Même chose pour
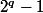
.
C'est bon?
Merci! :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 20 Nov 2005, 19:26
par Zebulon » 20 Nov 2005, 19:26
Super!!! :++:
A bientôt,
Zeb.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 20 Nov 2005, 19:31
par Zebulon » 20 Nov 2005, 19:31
En fait, c'est presque super:dans le diviseur composé de la grosse somme, il faut remplacer a par
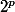
(tu as oublié la puissance p). De même pour l'autre divisibilité. Mais ça ne change pas les diviseurs qu'on voulait:
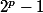
et
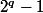
.
Zeb
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 20 Nov 2005, 20:25
par skyskiper » 20 Nov 2005, 20:25
Zebulon a écrit:En fait, c'est presque super:dans le diviseur composé de la grosse somme, il faut remplacer a par
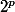
(tu as oublié la puissance p). De même pour l'autre divisibilité. Mais ça ne change pas les diviseurs qu'on voulait:
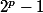
et
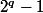
.
Zeb
Ah oui! Roudioudiou, on mettra ça sur le compte de la fatigue! lol :id2:
Merci encore!!! :ptdr:
++
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
.
(tu as oublié la puissance p). De même pour l'autre divisibilité. Mais ça ne change pas les diviseurs qu'on voulait:
et
.