Divisibilité

[joq35]

Bonjour,

Je dois montrer que 2^n - 1 est divisible par 7 si et seulement si n est un multiple de 3. En supposant que n est un multiple de 3, j'arrive à démontrer que 2^n - 1 est divisible par 7. Par contre, dans l'autre sens, je sèche. Pouvez-vous me mettre sur la piste ?

Merci à vous

[catamat]

Bonjour
On peut montrer que si n n'est pas multiple de 3 alors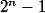 n'est pas multiple de 7 soit la contrapposé de ce que tu cherches à démontrer.

[Ben314]

Salut,
Tu peut aussi montrer que le reste de la division par 7 de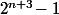 est le même que celui de 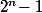(ce qui est facile vu qu'il suffit de montrer que la différence des deux est un multiple de 7).
Donc le reste de la division par 7 de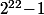 est le même que celui de 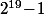qui est le même que celui de 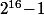etc qui va être le est le même que celui de 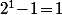donc 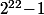n'est pas divisible par 7.

[joq35]

Merci à vous deux.
Je m'en suis sorti avec la contraposée. Par contre, pouvait-on le démontrer "en mode direct" ? C'est-à-dire supposer que 2^n -1 est divisible par 7. Et montrer que n est multiple de 3 .

[joq35]

Pour la contraposée, voici ce que j'ai fait :
On suppose n congru à 1 modulo 3. Donc n = 3k+1.
D'où 2^(n) = 2^(3k) * 2 = (2^3)^k * 2
Or 2^3 est congru à 1 modulo 7. Donc (2^3)^k * 2 est congru à 2 modulo 7. Ainsi, 2^n-1 n'est pas divisible par 7.

On fait de même pour n congru à 2 modulo 3. Et on conclut. Mais la méthode directe m’intéresserait. Il y a la méthode de Ben314, mais il n'y a pas une façon de démontrer directement ?

[Ben314]

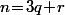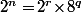Si tu connait les congruences, alors c'est extrêmement simple : tu effectue la division euclidienne de par 3 : avec puis tu écrit que est congru à 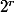modulo 7 vu que 8 est congru à 1 modulo 7. Donc,
- Si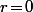 , alors 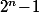est congru modulo 7 à .
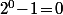- Si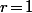 , alors 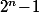est congru modulo 7 à .
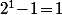- Si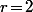 , alors 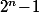est congru modulo 7 à .
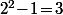Et tu constate que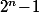 est divisible par 7 si et seulement si 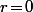, c'est à dire si et seulement si est divisible par 3.

Et concernant la preuve que je suggérais, c'est celle qu'on ferait dans le cas où on ne connait pas les congruences :
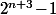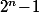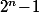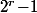est évidement multiple de 7 donc et ont même reste de division par 7. Puis une mini récurrence permet d'en déduire que, si est le reste de la division de par 3, alors et ont même reste de division par 7. ET tu conclue comme ci dessus.

[joq35]

Super merci beaucoup.