Divisibilité d'un produit de termes consécutifs
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 13 Mar 2010, 03:41
par Dinozzo13 » 13 Mar 2010, 03:41
Bonjour, aujourd'hui je me suis remet à l'arithmétique et donc, suite à quelque expériences sur la divisibilité de produits de nombres entiers successifs, je viens vous soumettre une formule généraliste concernant la divisibilité d'un produit d'entiers consécutifs.
On se donne un nombre

défini pour tout
\in\mathbb{Z}^3)
tel que

par :
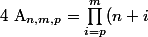)
Après quelque essais, je suis parvenu à la conclusion que :
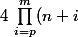\equiv 0 \left[ (|m-p|+1)! \right])
ou bien que
!)
divise
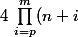)
.
Cela parraît-il correct ?
Merci d'avance ^^.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 13 Mar 2010, 03:43
par Dinozzo13 » 13 Mar 2010, 03:43
Pour info, je me suis appuyé sur quelque exemple :
(n-1)n(n+1) est divisible par 2 et 3 donc par 6
n(n+1)(n+2)(n+3)(n+4) est divisible par 5!=120
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 13 Mar 2010, 08:17
par Zweig » 13 Mar 2010, 08:17
Salut,
Ta conjecture est correcte, c'est un résultat "classique" en Arithmétique (j'entends par connu).
En ce qui concerne la démonstration, cela utilise le fait que les coefficients binôminaux sont entiers.
En effet, remarque que
}{(m-p+1)!} = \begin{pmatrix} n \\ m-p+1 \end{pmatrix})
Si ces nombres sont tous négatifs, on prend leur opposé. Sinon, c'est que l'un d'eux est nul, donc le produit est nul, qui est bien un entier.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 13 Mar 2010, 20:10
par Dinozzo13 » 13 Mar 2010, 20:10
Oh lala, ca fait du bien ^^ de conjecturer des trucs surtout en arithmétique.
Perso, ca va peut-être vous faire rire, en tout cas moi oui mais, je trouve que l'arithmétique est un raisonnement très puissant :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités