Bonjour,
on a corrigé un exo en classe que je n'ai pas du tout compris:
Trouvez La Directrice,Le Foyer,L'Axe De Symétrie et Le Sommet de la courbe suivante:
Y=3x²/2
Alors la directrice c'est Y=-1/6
Donc le foyer (0;1/6)
L'axe de symétire: x=0
Sommet (0;0)
SVP est-ce que quelqu'un peut m'expliquer clairement comment on a trouvé tout ça ?
merci d'avance,
ciao.
Directrice, foyer & cie ...
4 messages
- Page 1 sur 1
Bonjour
Dans un repère orthonormé du plan;la corbe d' équation
.............x² = 2py ou y= x² / 2p
est une PARABOLE
- de FOYER F(0;p/2)
- DIRECTRIECE y = - p/2
- d' AXE dec SYMETRIE x=0
- de SOMMET 0(o;o)
Tu as y = 3x²/2 = x² /( 2 *1/3) => p= 1/3
On a une PARABOLE de
-FOYER F(0:1/6)
-DIRECTRICE y = - 1/6
-Axe de symétrie x=0
-Sommet (0;0)
Dans un repère orthonormé du plan;la corbe d' équation
.............x² = 2py ou y= x² / 2p
est une PARABOLE
- de FOYER F(0;p/2)
- DIRECTRIECE y = - p/2
- d' AXE dec SYMETRIE x=0
- de SOMMET 0(o;o)
Tu as y = 3x²/2 = x² /( 2 *1/3) => p= 1/3
On a une PARABOLE de
-FOYER F(0:1/6)
-DIRECTRICE y = - 1/6
-Axe de symétrie x=0
-Sommet (0;0)
Bonjour, voici quelques explications supplémentaires...
Y=3x²/2 est l'équation d'une parabole.
La parabole est une des trois coniques (qui sont la parabole, l'hyperbole et l'ellipse). Elle a plusieurs définitions possibles. L'une d'elle est la suivante :
Etant donné un point F appelé foyer et une droite D appelée directrice, la parabole de foyer F et de directrice D est l'ensemble des points situés à égale distance du foyer et de la directrice. Si la directrice est parallèle à l'axe Ox, alors l'équation est facile à trouver.
Si x0,y0 sont les coordonnées du point F, y=y1, l'équation de D, alors le carré de la distance d'un point M(x,y) à F est (x-x0)²+(y-y0)² et le carré de la distance de ce point M à la directrice est tout simplement (y-y1)². Donc l'équation de la parabole, dans ce cas simple, est :
(x-x0)²+(y-y0)²=(y-y1)²
soit :
x²-2xx0+x0²+y²-2yy0+y0²=y²-2yy1+y1²
ou, en simplifiant et regroupant un peu :
x²-2xx0+2y(y1-y0)+x0²+y0²-y1²=0
Seul x figure au carré : on peut mettre l'équation sous la forme :
})
C'est l'équation générale d'une parabole dont la directrice est parallèle à Ox.
Pour trouver les trois valeurs inconnues : x0, y0 et y1, il suffit d'identifier les coefficients :
})
})x^2+(\frac{-2x_0}{2(y_0-y_1)})x+(\frac{x_0^2+y_0^2-y_1^2}{2(y_0-y_1)}))
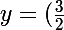x^2+0\times x + 0)
D'où :
})=(\frac{3}{2}))
})=0)
})=0)
De la première équation, tu peux tirer :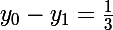
De la deuxième tu tires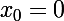
Et de la troisième tu extrais :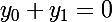
Finalement,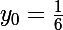 et
et 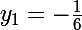
Le foyer a pour coordonnées :)
La directrice a pour équation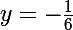
Y=3x²/2 est l'équation d'une parabole.
La parabole est une des trois coniques (qui sont la parabole, l'hyperbole et l'ellipse). Elle a plusieurs définitions possibles. L'une d'elle est la suivante :
Etant donné un point F appelé foyer et une droite D appelée directrice, la parabole de foyer F et de directrice D est l'ensemble des points situés à égale distance du foyer et de la directrice. Si la directrice est parallèle à l'axe Ox, alors l'équation est facile à trouver.
Si x0,y0 sont les coordonnées du point F, y=y1, l'équation de D, alors le carré de la distance d'un point M(x,y) à F est (x-x0)²+(y-y0)² et le carré de la distance de ce point M à la directrice est tout simplement (y-y1)². Donc l'équation de la parabole, dans ce cas simple, est :
(x-x0)²+(y-y0)²=(y-y1)²
soit :
x²-2xx0+x0²+y²-2yy0+y0²=y²-2yy1+y1²
ou, en simplifiant et regroupant un peu :
x²-2xx0+2y(y1-y0)+x0²+y0²-y1²=0
Seul x figure au carré : on peut mettre l'équation sous la forme :
C'est l'équation générale d'une parabole dont la directrice est parallèle à Ox.
Pour trouver les trois valeurs inconnues : x0, y0 et y1, il suffit d'identifier les coefficients :
D'où :
De la première équation, tu peux tirer :
De la deuxième tu tires
Et de la troisième tu extrais :
Finalement,
Le foyer a pour coordonnées :
La directrice a pour équation
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
