Difficulté sur les limites de fontion

par **Dinozzo13** » 23 Aoû 2010, 15:43

Dinozzo13 a écrit:Ravi de te revoir ^^

la limite en une valeur interdite nous donne l'infini à gauche et à droite donc la courbe C admet ...

une asymptote verticale d'équation ...

par **Dinozzo13** » 23 Aoû 2010, 15:44

Krapoplate a écrit:Oups, les asymptotes^j'avais completement zapé^^, Oui c'est une asymptote verticale, car la droite d'équation x=2 est asymptote verticale a la courbe Cf en + l'infini, par valeur inférieur et supérieur

Exact ! Et oui, les études de fonctions c'est tout des p'tits détail ^^, tu peux continuer :++:

par **Krapoplate** » 23 Aoû 2010, 15:46

^^ je vois que mon calcule par somme pose un certain mystère^^. Dans l'énoncé il m'a été demandé de dire par quelle opération j'arriverai à mon résultat, c'est à dire soit par somme soit par produit (ce sont les 2 opérations que j'ai vu en cours car il nous manquait du temps malheureusement pour cloturer notre chapitre). Donc il l'opération par somme, était le calcule attendu ;) car il n'y a pas de produit dans la fonction^^

par **Dinozzo13** » 23 Aoû 2010, 16:00

Par contre, 'va falloir que tu me dises où on en est :ptdr:

par **Krapoplate** » 23 Aoû 2010, 16:08

Ensuite pour le 3°)
j'ai tout mis au meme dénominateur dans l'expression f(x)= -x+1+(x-1)/(x-2)²

donc, f(x)= (-x)(x-2)²/(x-2)² + (x-2)²(1)/ (x-2)² + (x-1)/(x-2)²
F(x)= (-x^3-4x)/ (x-2)² + (x²+4)/(x-2)² + (x-1)/(x-2)²
f(x) = -x^3+x²+3x+3/ (x-2)²

Et voila ce que j'apelle un résultat désespérent, car je ne retombe pas sur l'expression donné au début .

par **Krapoplate** » 23 Aoû 2010, 16:09

Dinozzo13 a écrit:Par contre, 'va falloir que tu me dises où on en est :ptdr:

On est au 3°

par **Krapoplate** » 23 Aoû 2010, 16:14

Pour la suite y=-x+1 est asymptote oblique par rapport a la courbe C

par **Dinozzo13** » 23 Aoû 2010, 16:21

As-tu étudier le sens de variation de f ainsi que son tableua de variations ?

par **Krapoplate** » 23 Aoû 2010, 16:26

Alors pour le tableau de variation de f
f est décroissant sur ]- l'infini; 1[, puis croissante sur ]1;2[ ( a noter qu'il y a une double barre sous 2 car c'est une valeur interdite), et ensuite f est décroissante sur ]2; + l'infini[

par **Dinozzo13** » 23 Aoû 2010, 16:35

Avec, dans le tableau f(1)=0

Donc démontre que

est asymptote oblique

par **Krapoplate** » 23 Aoû 2010, 16:47

Je dirais qu'en dressant le tableau de variation de y=-x+1, nous constatons que cette droite tend vers - l'infini en + l'infini comme pour -x^3+5x²-7x+3/(x-2).
Ensuite, lorsque y=-x+1 tend vers - l'inifini, x tend vers + l'infini. Tout comme la courbe C
Enfin, comme pour f(x), y = -x+1, la droite passe par les coordonnées (1;0).
DOnc grace à ces indications nous constaton qu'il y a une corrélation, soit un parallélisme entre C et y=-x+1. D'ailleurs , l'asymptote est oblique du faite que lorsque la courbe et la droite tendent vers - l'infini, x tend vers + linfini, et la fin de la courbe se tend en + l'inifini. Donc si on pouvait relier les points on contaterait qu'il y a une diagonale ( c'est confus mon explication)

par **Dinozzo13** » 23 Aoû 2010, 16:55

Oui c'est vrai :ptdr:

Il y a plus simple, sers toi de ce qu'on a montré précédement :
Pour tout x de

, on a montré que :

Or d'après ton cours, une droite d d'équation ax+b est asymptote oblique à une courbe reprsentative si et seulement si :

par **Krapoplate** » 23 Aoû 2010, 17:00

Oula, oui j'avoue que ça fait très raccourci^^. Mais Je n'est jamais vu ça dans mes cours enfin avec la dernière propriété. En fait on a pas vu grand chose sur les asymptotes :s. Cela dit je ne comprend pas cette propriété.

par **Dinozzo13** » 23 Aoû 2010, 17:02

'Y a pas grand chose à comprendre c'est comme ça à appliquer :zen:

par **Krapoplate** » 23 Aoû 2010, 17:12

Bon alors voila ce que je trouve :s

lim[(x-1)/(x-2)²]=lim [(x-1)/(x-2)²]=0
x->-l'infini x-> + l'infini

par **Dinozzo13** » 23 Aoû 2010, 17:14

Donc pour montrer que la droite \Delta d'équation y= -x+1 est asymptote oblique à C, il faut montrer que :

Pour cela utilise :

par **Krapoplate** » 23 Aoû 2010, 17:15

On peut résoudre l'équation a savoir
(x-1)/(x-2)²=(x-1)/(x-2)²
0=(x-1)/(x-2)² - ((x-1/(x-2)²)

par **Dinozzo13** » 23 Aoû 2010, 17:16

Oui, c'est ça donc

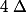
est ... (je te laisse rédiger :++:)

Ensuite : Etudie la position relative de C et

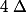
, un problème pour ça ?

par **Dinozzo13** » 23 Aoû 2010, 17:19

Krapoplate a écrit:On peut résoudre l'équation a savoir
(x-1)/(x-2)²=(x-1)/(x-2)²
0=(x-1)/(x-2)² - ((x-1/(x-2)²)

Oula non, là c'est du charabia ^^

Sers toi de la propriété sur les limites de fonction rationnelles en + et - l'infini :

Et voilà, tout simplement

par **Krapoplate** » 23 Aoû 2010, 17:22

Donc, y= -x+1 est asymptote oblique a la courbe Cf .

Donc nous pouvons dire que C est parallèle à y= -x+1. (j'espère que c'est ça la position relative)

Difficulté sur les limites de fontion

Qui est en ligne