Bonjour à tous,
Je dois rendre un devoir sur les fonctions dérivées mais certaines me posent problèmes car ne contenant pas de x je ne sais pas si elles relèvent d'une fonction.
Voici les trois fonctions que je n'arrive pas à dériver:
f(x)= (6x^2 - 5x + 1) / 3
f(x) = (8 / x^2)+ (x^2 / 8)
f(x)= 1 - 3x - (4 / 3x + 1)
Votre aide me serait précieuse, merci d'avance!
Devoir sur les fonctions dérivées
12 messages
- Page 1 sur 1
Mutugui a écrit:Bonjour à tous,
Je dois rendre un devoir sur les fonctions dérivées mais certaines me posent problèmes car ne contenant pas de x je ne sais pas si elles relèvent d'une fonction.
Voici les trois fonctions que je n'arrive pas à dériver:
f(x)= (6x^2 - 5x + 1) / 3
f(x) = (8 / x^2)+ (x^2 / 8)
f(x)= 1 - 3x - (4 / 3x + 1)
Votre aide me serait précieuse, merci d'avance!
-------------------------------------------------------------------------------
Salut,
tu n'a pas essayé (u/v)' = (u'.v-u.v')/v² ?
on est pas loin....
Pour dériver f(x)= (6x^2 - 5x + 1) / 3, mets la constante 1/3 "de côté" comme ceci :
f(x)= (6x^2 - 5x + 1) / 3 =(1/3)*(6x²-5x+1).
Alors f est de la forme k*u avec k constante et u une fonction, donc f'=k*u' ce qui te donne :
f'(x)=(1/3)*(la dérivée de 6x²-5x+1).
La question est : sais-tu dériver le polynôme 6x²-5x+1 ? Il faut connaître la formule pour dériver x^n : (x^n)'=n*x^(n-1).
Pour dériver f(x) = (8 / x^2)+ (x^2 / 8), mets aussi les constantes de côté :
f(x) = (8 / x^2)+ (x^2 / 8)=8*(1/x²)+(1/8)*x² et quand tu dérives tu gardes les constantes et tu dérives les fonctions.
Pour dériver (4 / 3x + 1), tu mets 4 de coté : (4 / 3x + 1)=4*1/(3x+1) et tu laisses 4 et tu dérives 1/(3x+1) [de la forme 1/v voir la formule correspondante].
Commence déjà par là et retiens ce principe de mettre la constante (qui te gêne) de côté !
Si ça te dit de visiter mon blog de maths : exercices de maths en vidéo
f(x)= (6x^2 - 5x + 1) / 3 =(1/3)*(6x²-5x+1).
Alors f est de la forme k*u avec k constante et u une fonction, donc f'=k*u' ce qui te donne :
f'(x)=(1/3)*(la dérivée de 6x²-5x+1).
La question est : sais-tu dériver le polynôme 6x²-5x+1 ? Il faut connaître la formule pour dériver x^n : (x^n)'=n*x^(n-1).
Pour dériver f(x) = (8 / x^2)+ (x^2 / 8), mets aussi les constantes de côté :
f(x) = (8 / x^2)+ (x^2 / 8)=8*(1/x²)+(1/8)*x² et quand tu dérives tu gardes les constantes et tu dérives les fonctions.
Pour dériver (4 / 3x + 1), tu mets 4 de coté : (4 / 3x + 1)=4*1/(3x+1) et tu laisses 4 et tu dérives 1/(3x+1) [de la forme 1/v voir la formule correspondante].
Commence déjà par là et retiens ce principe de mettre la constante (qui te gêne) de côté !
Si ça te dit de visiter mon blog de maths : exercices de maths en vidéo
Merci de vos réponses!
Pour la 1ère dérivée je trouve: 1/3 x (12x - 5)
En revanche je bloque toujours pour les 2 autres. Comment résoudre 8 x 1/x^2 ?
Et pour la dernière il m'est demandé de démontrer que pour tout réel différent de -1/3 on a f'(x) = 9(-3x^2 - 2x + 1) / (3x + 1)^2 . Je ne sais plus comment multiplier des fractions...
Pour la 1ère dérivée je trouve: 1/3 x (12x - 5)
En revanche je bloque toujours pour les 2 autres. Comment résoudre 8 x 1/x^2 ?
Et pour la dernière il m'est demandé de démontrer que pour tout réel différent de -1/3 on a f'(x) = 9(-3x^2 - 2x + 1) / (3x + 1)^2 . Je ne sais plus comment multiplier des fractions...
[quote="Mutugui"]Merci de vos réponses!
Pour la 1ère dérivée je trouve: 1/3 x (12x - 5)
En revanche je bloque toujours pour les 2 autres. Comment résoudre 8 x 1/x^2 ?
Et pour la dernière il m'est demandé de démontrer que pour tout réel différent de -1/3 on a f'(x) = 9(-3x^2 - 2x + 1) / (3x + 1)^2 . Je ne sais plus comment multiplier des fractions...[/QUOTE]
-----------------------
Bonsoir,
1) oui et on peut l'écrire aussi : f(x) = 4x -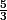
2) f(x)= +
+ 
=
f'(x)=-((64+x^4).16x)}{64x^4})
f'(x)=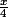 -
- 
3)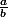 x
x  =
= 
----------------------------------
je vois que tu bloques.....
f'(x)=-3-^2}) = -3 +
= -3 + ^2})
f'(x) =+12}{(3x+1)^2})
je te laisse finir pour obtenir la factorisation souhaitée, à savoir 9(-3x²-2x+1) au numérateur.....
Pour la 1ère dérivée je trouve: 1/3 x (12x - 5)
En revanche je bloque toujours pour les 2 autres. Comment résoudre 8 x 1/x^2 ?
Et pour la dernière il m'est demandé de démontrer que pour tout réel différent de -1/3 on a f'(x) = 9(-3x^2 - 2x + 1) / (3x + 1)^2 . Je ne sais plus comment multiplier des fractions...[/QUOTE]
-----------------------
Bonsoir,
1) oui et on peut l'écrire aussi : f(x) = 4x -
2) f(x)=
=
f'(x)=
f'(x)=
3)
----------------------------------
je vois que tu bloques.....
f'(x)=-3-
f'(x) =
je te laisse finir pour obtenir la factorisation souhaitée, à savoir 9(-3x²-2x+1) au numérateur.....
Mutugui a écrit:Je trouve au final f'(x)= (16x^5 - 1024) / 64x^4 Est-ce correct?
Pour 1 - 3x - 4/ 3x+1 je ne trouve pas ce qui est demandé...
Je dois de plus faire le tableau de signe de f'(x)= 5/2racinecarréde x + 2 mais bloque complètement. Si vous pouviez me guider...
Merci beaucoup!
--------------------------------
Je trouve au final f'(x)= (16x^5 - 1024) / 64x^4 Est-ce correct?
--------------------------------
ça n'est pas -1024 x ?.....
ce qui te ferait retomber sur
-----------------------------
C'est le tableau de signe de f'(x)=
Mutugui a écrit:Oh oui erreur de ma part, pardon... J'ai du mal à comprendre la simplification en revanche...
Non c'est le 2 s'ajoute à la fraction entière.
-----------------------------------------------------------------
Est-ce f'(x)=
Tu vois comme quoi il est hyper important de bien écrire sinon on va droit dans le mur !!!...
Mutugui a écrit:En effet j'obtiens bien cela en utilisant la formule u/v mais j'avais au début pris 4 comme une constante.
J'ai finalement réussi à faire mes tableaux de variations pour chacune des fonctions.
Je vous remercie beaucoup de votre aide.
Bonne soirée à vous!
---------------------------------------
A ton service, content que tout soit ok pour toi !
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
