Devoir seconde à confirmer SVP

[axouten]

Bonsoir à tous,
J'ai fait la partie numération de mon DM mais je ne me suis pas arraché les cheveux pour une fois alors j'ai bien peur d'avoir tout faux. Pouvez- vous vérifier SVP ? Merci d'avance.

En déduire je trouve

Ecrire l'inverse de je trouve

Ecrire en utilisant seulement des nombres premiers élevés à des puissances positives :

je trouve

je trouve 600

je trouve

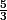
Factoriser x-5)^2-(2-7x)^2 je trouve (8x-7)(8x-7)
(2x-3)(x+4)-x(2x-3) je trouve 4(2x-3)

Voilà, je vous remercie de prendre le temps de relire tout ça. Bonne soirée à tous.

[Huppasacee]

bonsoir

oui, c'est bon

je trouve

encore bon

Ecrire l'inverse de je trouve

là , une erreur
c'est

qu'il faudra transformer pour avoir un dénominateur entier

je trouve

la fraction est bonne, mais décompose le numérateur en produit de facteurs premiers

je n'ai pas vérifié les autres , mais par exemple, pour 600, si c'est bien le résultat ( ta calculatrice te le dira ), il faut le décomposer en produit de puissances de 2 , 3 et 5

[axouten]

Merci, je vais refaire celui sur l'inverse et décomposer les autres en produits de facteurs premiers. Je reviendrais noter mes résultats. Bonne soirée et merci encore.

[axouten]

Bon alors j'ai repris l'inverse et je trouve pareil :
= \ = =

décomposé en produits de facteurs premiers

Même chose pour 600 =
Par contre est-ce que vous pouvez me dire si mes factorisations sont justes SVP.
Merci encore. Bonne soirée.

[Huppasacee]

= = =

bonsoir

tu as remis le même résultat!
vérifie ton identité remarquable au dénominateur !

pour obtenir un nombre entier au dénominateur, il faut multiplier par la " quantité conjuguée "

pour mémoire :

(a + b)² = ?

et

(a + b)(a - b) = ?

sinon, le reste est correct