Devoir passerelle: SOS

par **code47** » 09 Aoû 2006, 14:19

Bonjour tt le monde,
au lycée on m'a filé des exercices à faire pdt les vacances et qui seront notés et il y en a un qui me pose problème. C'est des équations à résoudre dans R mais c'est un truc que j'ai vu en début de seconde et que je sais plus faire et j'ai plus mes cours. Ca serait super que quelqu'un puisse m'aider.
voila les équations:

(x-2)² = 1/16(5-2x)²

4(x+3)²-9(2x-1)(-x-3) = 0

Merci d'avance .

par **nox** » 09 Aoû 2006, 15:00

Il faut développer les expressions en utilisant les identités remarquables et ramener les équations sous la forme ax²+bx+c = 0 en regroupant les termes en x² et les termes en x.

Il suffit ensuite de résoudre en calculant

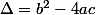
les solutions sont ensuite :

et

par **rene38** » 09 Aoû 2006, 15:08

Bonjour

code47 a écrit:...c'est un truc que j'ai vu en début de seconde ...

Je suppose donc que tu entres en première et que tu n'as pas encore vu la résolution proposée par nox.
Dans ce cas, il faut transformer tes équations pour les mettre sous la forme
un produit = 0
(factorisation utilisant les identités remarquables et/ou la recherche de facteur commun)
puis utiliser la propriété "Si ab=0 alors a=0 ou b=0"

par **code47** » 09 Aoû 2006, 18:19

thank's a tous :we:

par **code47** » 09 Aoû 2006, 19:21

chui dsl mais je n'arrive toujours pas à faire la première:

(x-2)² = 1/16(5-2x)²

alor si quelqu'un pouvais encore m'aider ca me rendrait un grand service
merci par avance

par **Sdec25** » 09 Aoû 2006, 19:29

Il faut mettre cette équation sous la forme d'un produit = 0
Rassemble déjà tout du même côté et factorise en t'aidant de l'identité remarquable a²-b² = (a+b)(a-b)

par **code47** » 09 Aoû 2006, 19:37

tu peu me montrer le début stp

par **Sdec25** » 09 Aoû 2006, 19:39

Pas de problème.
(x-2)² = 1/16(5-2x)²
(x-2)² - (1/4[5-2x])² = 0
A mettre sous la forme d'un produit qui est égale à 0.

par **nekros** » 09 Aoû 2006, 19:47

Bonjour,

On a :

Donc

et donc

On reconnaît une identité remarquable et on a :

Le produit est nul si l'un des facteurs est nul donc si :

ou

Thomas G :zen:

par **nox** » 09 Aoû 2006, 19:47

c'est malin nekros !! :ptdr:

sdec25 etait en train de le guider subtilement vers la solution et toi t'arrives avec ton char d'assaut :ptdr:

par **nekros** » 09 Aoû 2006, 19:48

Oups désolé Sdec, je n'avais pas vu que tu étais sur le coup :marteau:

Thomas G :zen:

par **code47** » 09 Aoû 2006, 19:49

aaaaahhhhhhhhh ok
en fait j'avais laisser 1/16 au lieu de mettre 1/4

merci BEAUCOUP
bye

par **nekros** » 09 Aoû 2006, 19:49

nox a écrit:c'est malin nekros !! :ptdr:

sdec25 etait en train de le guider subtilement vers la solution et toi t'arrives avec ton char d'assaut :ptdr:

Bah ouais, jsuis trop lent en LATEX.
Désolé Sdec d'avoir bousillé tes plans :briques:

Thomas G :zen:

par **nox** » 09 Aoû 2006, 19:50

l'essentiel c'est que code47 a compris ^^

mais on se fait souvent des duels de rapidité en LateX sur le forum avec Sdec25 :ptdr:

par **Sdec25** » 09 Aoû 2006, 19:52

Ouais c'est pas grave, du moment qu'il a compris :zen:
Mais pour ce genre d'exercice, entre donner un indice et donner la solution il n'y a qu'un pas :happy3:

Pour LateX, j'ai hésité à l'utiliser mais finalement je me suis dit qu'il pourrait déchiffrer mes 2 lignes sans trop de problème :we:

par **nekros** » 09 Aoû 2006, 19:54

Sdec25 a écrit:Mais pour ce genre d'exercice, entre donner un indice et donner la solution il n'y a qu'un pas :happy3:

La preuve... :ptdr:

Thomas G :zen:

Devoir passerelle: SOS

devoir passerelle: SOS

Qui est en ligne