Devoir Maison vecteur

[emma-54-78]

Bonjour à tous,
Voilà j'ai commencé mon DM mais il y a des questions où je suis bloquée :s
Voici l'énoncé :
On considère les points A(-2;5/2) et B(4;-1/2)

1) Déterminer les coordonnées du milieu I du segment [AB] ==> I (1;1)
2) Le vecteur u(-12/5;7/5) est-il coliénaire au vecteur AB? ==> J'ai trouvé qu'il ne l'était pas
4) Le point D(2;3) appartient-il à la médiatrice du segment [AB] ?==> il n'appartient pas

Voilà les réponses que j'ai trouvé pour les questions 1-2-4
Maintenant j'ai plus de mal pour les questions 3-5-6

3) Soit C le point de coordonnées( racine de 3;x )où x est un nombre réel.Déterminer x pour que le point C appartienne à la droite (AB).

Voilà alors ici je ne sais pas du tout quel calcul il faut appliquer pour trouver le point x ..



5)Le point E(1;-5/2) appartient-il au cercle de diamètre [AB]?

En faisant la construction j'ai bien vu qu'il appartenait à ce cercle mais là encore une fois je ne sais pas comment le démontrer


6) Calculer les coordonnées du point K tel que : (ce ne sont que des vecteurs que je vais noter) : KI - 3KE = 0


Voilà si quelqu'un est décidé à m'aider je lui en serais très reconnaissante :) !

[gigamesh]

Bonjour,
les questions sur lesquelles tu bloques nécessitent une approche particulière :
le raisonnement par équivalence.
En fait on ne sait pas comment calculer directement, car il n'y a pas de formule directe pour toutes les situations possibles !

Par contre, voila ce qu'on sait :
* on sait calculer les coordonnées de en fonction de
* on sait que si et seulement si A, B et C sont alignés
* on sait que des points sont alignés si des vecteurs sont colinéaires
* on sait traduire la colinéarité de deux vecteurs par une égalité
* on sait résoudre une équation

Pour la 5), on sait :
* qu'un point est sur un cercle si et seulement si il est à la bonne distance du centre
* calculer une distance dans un repère orthonormé

Pour la 6), on sait :
* choisir des inconnues : on dit que les coordonnées de K sont et
* exprimer les coordonnées de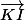 et
en fonction de et
* on sait que des vecteurs sont égaux si et seulement si ils ont les mêmes coordonnées

[emma-54-78]

merci beaucoup de ton aide! :happy2:

Oui c'est vrai je n'y avais pas pensé aux vecteurs colinéaires!
J'ai bien compris comment on procède mais le seul soucis c'est que je n'ai pas mon cours entier et il me manque la partie (évidemment..) sur la colinéarité ^^" donc pour traduire la colinéarité de deux vecteurs par une égalité je n' ai aucune idée de comment on procède :hein:
si tu pouvais m'éclairer :happy2:

pour la question 5) merci beaucoup pour cette info car on m'avais conseillé de résoudre l'équation du cercle mais ta méthode est plus facile ( du moins pour moi ^^ )

et pour la question 6) et bien écoutes j'ai essayé de résoudre et j'ai trouvé K (1;1/8) mais je n'ai pas pris ta méthode donc si tu peux me dire si tu trouves pareil ou pas sinon ça voudrait dire que je me suis certainement trompée :hein:

[gigamesh]

Pour les vecteurs colinéaires, c'est ultra simple !!

Des vecteurs sont colinéaires si et seulement si leurs coordonnées sont proportionnelles ... Ce qui se traduit par l'égalité des produits en croix !
Pas de grande nouveauté depuis le CM2, en fait !

Pour parler pointu, au lycée on écrit des trucs du genre :
et sont colinéaires ssi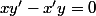

(et cette équivalence porte le doux nom de "condition analytique de colinéarité")

Pour la question 6), l'égalité peut se réécrire
donc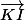 et ont le même sens ; par conséquent K ne peut pas être sur le segment [IE] ...
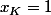Par contre K est sur (IE), l'équation de (IE) est juste , donc , la je suis d'accord.

[emma-54-78]

Bonjour!
Je suis très contente que tu puisses m'aider parce que je comprends bien quand tu m'expliques :id:

Enfin..je comprends bien comment il faut procèder et tout mais les calculs en revanche c'est pas trop ça :triste:
parce que pour la question 3) j'ai tout bien compris comment il fallait procéder avec la colinéarité et donc là j'essaie de calculer les coordonnées du vecteur AC pour après trouver si il est colinéaire au vecteur AB..(c'est bien ça? :happy2: )

Donc j'ai fait AC = (Xc-Xa;Yc-Ya)
donc je trouve (racine de 3 + 2 ; ? -5/2 )
et c'est là que je bloque :cry: je sais qu'il faut surement faire une équation pour trouver x mais je suis vraiment trop nul j'ai jamais réussi à mettre en équation des problèmes :cry:

[gigamesh]

Du calme et de la sérénité !
Mettre en équation, c'est traduire, et souvent c'est juste de la traduction mot-à-mot en plus.

Bon tu as déjà trouvé les coordonnées de et , c'est un bon début.

Voila ce qu'on a sous la main :
*
*
* la propriété du cours " et sont colinéaires si et seulement si 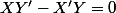" ; cette propriété s'appelle la "condition analytique de colinéarité" car elle nous dit à quelle condition des vecteurs sont colinéaires, à partir de leurs coordonnées (le mot analytique, ici, signifie "avec des coordonnées") ; cette propriété traduit une notion géométrique (la colinéarité) par une notion algébrique (l'égalité de deux nombres).

Voila ce qu'on veut : traduire cette histoire de colinéarité par une égalité, dans laquelle intervient x (bon c'est une équation quoi)

Le principe de base d'une équation, c'est la patience : on ne cherche pas LE calcul qui donne x ; on cherche juste une égalité avec x dedans, et après on résout. (Le "après" est important !).

Sans équations, on ne peut résoudre que des problèmes faciles dans lesquels on "voit" tout de suite quels calculs faire, et dans quel ordre, pour arriver au résultat.

Alors qu'ici on se fiche des calculs à faire ; on veut juste écrire une égalité qui traduit la situation.

Bon, assez causé :

et sont colinéaires si et seulement si ..... - ........ = 0

Je te laisse finir...

[emma-54-78]

Merci beaucoup du temps que tu prends pour m'aider :++: :we:

Alors je pense que c'est :
AB(6;-3) et AC (racine de 3 + 2; x -2.5) sont colinéaires si et seulement si
(6 "fois" x-2.5)-(racine de 3 +2 "fois" -3) = 0

(désolé pour les "fois" mais avec les x je savais pas comment faire :hum: )

c'est bon? :id:

[gigamesh]

Comment dire ?
Je suis d'accord avec ce que tu as voulu écrire, mais pas avec ce que tu as écrit !
Oui je sais, c'est bizarre...

Bon plus concrètement, tu as écrit l'équation

mais ce que tu voulais (et devais) écrire
était
ce qui n'est pas la même chose.

Bon une fois que les parenthèses sont au bon endroit, tu as une magnifique équation, tu n'as plus qu'à la résoudre !

Quelques indications : développe, réduis, soustrait aux deux membres, ajoutes 9 aux deux membres, il ne reste qu'à diviser par 6 !
Bon dans la solution, il reste une racine mais c'est normal, on te demande la valeur exacte.

Au fait pour la multiplication tu peux utiliser * comme sur un tableur (c'est une notation américaine). Sinon, tu peux te mettre à TEX, qui permet d'écrire des maths très joliment ; il y a un tutoriel sur le site :
http://maths-forum.com/showthread.php?t=70548

[emma-54-78]

Oh..oui c'est vrai t'as raison ! ^^"

Bon alors je me lance!! (et avec l'écriture TEX :zen: )


==> développer

==> réduire

==>soustraire

Jusqu'ici est-ce bon? parce que avec les indications que tu m'as donné j'arrive pas du tout à voir pourquoi tu m'as dis d'ajouter un 9? parce que dans mon équation j'en ai pas :hein:

[gigamesh]

Tu y es presque !

Tu as écrit :

mais avec , et
donc


Du coup en développant l'équation devient


puis



Et voila le 9 dont je te parlais.

Presque fini !

[emma-54-78]

Ah d'accord oui je vois c'est vrai que des trucs comme ça j'y pense jamais pour moi c'est pas évident de voir ça ^^"

Okay donc du coup ça fait :




C'est bon? :id:
et donc après si on repend tout depuis le début maintenant que l'on a x, on peut calculer les coordonnées des deux vecteurs AC et AB , et savoir s'ils sont colinéaires? :happy2: et donc si ils le sont cela voudra dire que C est aligné avec A et B!

[gigamesh]

Oui, c'est ça ; bon on peut simplifier un peu :



(on applique le principe RTC : range ta chambre).

Pour la vérification, c'est toujours une bonne idée de la faire, histoire d'être sûr qu'on n'a pas fait d'erreur de calcul ou de méthode.
Par contre, mathématiquement, elle n'est pas indispensable ici car on a raisonné par équivalence, c'est-à-dire que chaque étape du raisonnement est une condition nécessaire et suffisante pour la précédente et la suivante ; si tu veux on peut dire qu'à chaque étape on a dit si "telle ligne" alors on a "la ligne suivante", et réciproquement .

Mais ça serait dommage de se priver d'une belle occasion de faire quelques calculs !

Bravo pour ta persévérance, comme tu vois ça paye !

[emma-54-78]

Merci beaucoup de ton aide!!! :we:
Vraiment c'est super!!
Pour les coordonnées de AC je trouve :

et AB

après j'ai fais xy'-yx'=



et quand je fais en décimal ça me fait 0,86 :hum: alors que pour qu'il soit colinéaire faut que ça fasse 0

[gigamesh]

Encore un peu de courage !

a pour coordonnées donc soit

Tu as aussi une erreur de signe pour l'ordonnée du vecteur ; tu trouves 3, mais regardes la figure : le vecteur part vers la droite (de -2 à 4 en abscisses) et vers le bas (de 5/2 à -1/2).
Vers la droite donc son abscisse est positive ().
Mais comme le vecteur descend, son ordonnée doit être négative !

Enfin, pour les parenthèses, elles sont mal placées ; tu as écrit
;
mais ce que tu voulais écrire était :


Et après corrections des coordonnées des deux vecteurs, on obtient

et le calcul va nous donner zéro !
Moralité, attention aux signes, et à bien placer les parenthèses.

[emma-54-78]

Oula oui j'ai refais les coordonnées tu as raison j'avais mal mis le signe!
c'était AB (6;-3)

De tout façon ça j'ai toujours eu un soucis avec les parenthèses et les signes c'est toujours des erreurs d'innatention qui me coute des points :triste:


Et alors pour xy'-yx' =
Quand c'est marqué ou
cela veut dire que l'on prend tout l'ensemble de la parenthèse et que l'on multiplie tout par ce nombre?

C'est juste une petite remise en mémoire ^^'
Parce que j'ai fais comme ça et à un moment il y a deux 12 donc je simplifie et après il me reste

Ce qui me donne -0.8 :triste:

[gigamesh]

il y a deux 12 ?
Hum... à un moment il y a un 12, oui, dans
Mais pas deux ! Si tu calcules
c'est .

Multiplier une fraction par 6, c'est multiplier le numérateur par 6, mais pas le dénominateur !

De plus, quelque chose du genre ne se simplifie pas en , car l'expression signifie "je prends un nombre a, j'ajoute 12 puis je divise par 12". La division n'est pas le contraire de l'addition.

Bon le plus simple pour calculer , c'est d'utiliser la propriété :


Je te laisse finir.

[emma-54-78]

:happy2: Ah bin oui c'est pour ça que je trouvais deux fois 12!! ^^" oulala je suis désolé hun c'est vrai que j'ai fais une énorme erreur la :s

J'ai tout recalculé et là ça y est enfin c'est booooon!!!! :we:
Je trouve 0 !!! :zen:

Merci beaucoup beaucoup de ton aide!! :we: :we: :we:


Et en plus j'ai trouvé la question 6) aussi on l'avait un peu oublié mais j'ai trouvé les coordonnées de K!! et puis c'est bon parce que j'ai vérifié :we:
C'est

Je suis trop contente on a enfin fini :happy2: Encore merci pour ton aide !

[gigamesh]

Bravo ! :zen: